| << Chapter < Page | Chapter >> Page > |
Another type of tube is one that is open at both ends. Examples are some organ pipes, flutes, and oboes. The resonances of tubes open at both ends can be analyzed in a very similar fashion to those for tubes closed at one end. The air columns in tubes open at both ends have maximum air displacements at both ends, as illustrated in [link] . Standing waves form as shown.
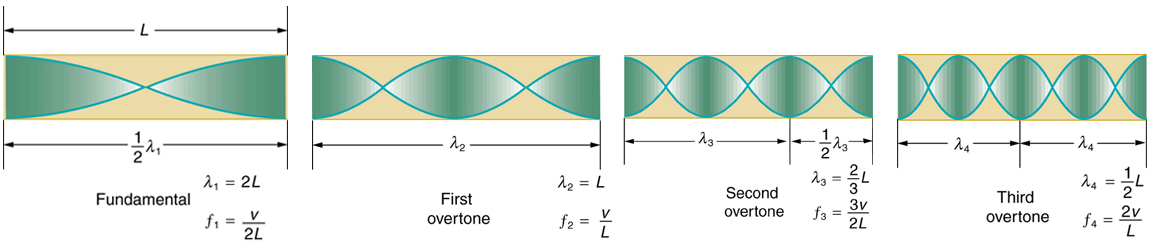
Based on the fact that a tube open at both ends has maximum air displacements at both ends, and using [link] as a guide, we can see that the resonant frequencies of a tube open at both ends are:
where is the fundamental, is the first overtone, is the second overtone, and so on. Note that a tube open at both ends has a fundamental frequency twice what it would have if closed at one end. It also has a different spectrum of overtones than a tube closed at one end. So if you had two tubes with the same fundamental frequency but one was open at both ends and the other was closed at one end, they would sound different when played because they have different overtones. Middle C, for example, would sound richer played on an open tube, because it has even multiples of the fundamental as well as odd. A closed tube has only odd multiples.
Resonance occurs in many different systems, including strings, air columns, and atoms. Resonance is the driven or forced oscillation of a system at its natural frequency. At resonance, energy is transferred rapidly to the oscillating system, and the amplitude of its oscillations grows until the system can no longer be described by Hooke’s law. An example of this is the distorted sound intentionally produced in certain types of rock music.
Wind instruments use resonance in air columns to amplify tones made by lips or vibrating reeds. Other instruments also use air resonance in clever ways to amplify sound. [link] shows a violin and a guitar, both of which have sounding boxes but with different shapes, resulting in different overtone structures. The vibrating string creates a sound that resonates in the sounding box, greatly amplifying the sound and creating overtones that give the instrument its characteristic flavor. The more complex the shape of the sounding box, the greater its ability to resonate over a wide range of frequencies. The marimba, like the one shown in [link] uses pots or gourds below the wooden slats to amplify their tones. The resonance of the pot can be adjusted by adding water.


Notification Switch
Would you like to follow the 'College physics ii' conversation and receive update notifications?