| << Chapter < Page | Chapter >> Page > |
Would the previous question make any sense for an isochoric process? Explain your answer.
We ordinarily say that for an isothermal process. Does this assume no phase change takes place? Explain your answer.
The temperature of a rapidly expanding gas decreases. Explain why in terms of the first law of thermodynamics. (Hint: Consider whether the gas does work and whether heat transfer occurs rapidly into the gas through conduction.)
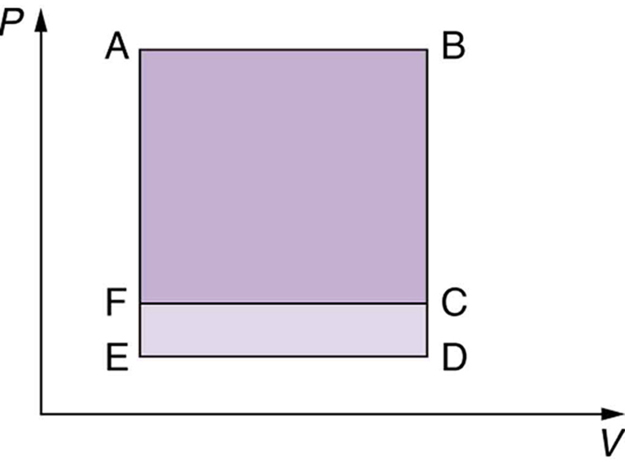
Which cyclical process represented by the two closed loops, ABCFA and ABDEA, on the diagram in the figure below produces the greatest net work? Is that process also the one with the smallest work input required to return it to point A? Explain your responses.
A real process may be nearly adiabatic if it occurs over a very short time. How does the short time span help the process to be adiabatic?
It is unlikely that a process can be isothermal unless it is a very slow process. Explain why. Is the same true for isobaric and isochoric processes? Explain your answer.
A car tire contains of air at a pressure of (about 32 psi). How much more internal energy does this gas have than the same volume has at zero gauge pressure (which is equivalent to normal atmospheric pressure)?
A helium-filled toy balloon has a gauge pressure of 0.200 atm and a volume of 10.0 L. How much greater is the internal energy of the helium in the balloon than it would be at zero gauge pressure?
Steam to drive an old-fashioned steam locomotive is supplied at a constant gauge pressure of (about 250 psi) to a piston with a 0.200-m radius. (a) By calculating , find the work done by the steam when the piston moves 0.800 m. Note that this is the net work output, since gauge pressure is used. (b) Now find the amount of work by calculating the force exerted times the distance traveled. Is the answer the same as in part (a)?
(a)
(b) . Yes, the answer is the same.
A hand-driven tire pump has a piston with a 2.50-cm diameter and a maximum stroke of 30.0 cm. (a) How much work do you do in one stroke if the average gauge pressure is (about 35 psi)? (b) What average force do you exert on the piston, neglecting friction and gravitational force?
Calculate the net work output of a heat engine following path ABCDA in the figure below.
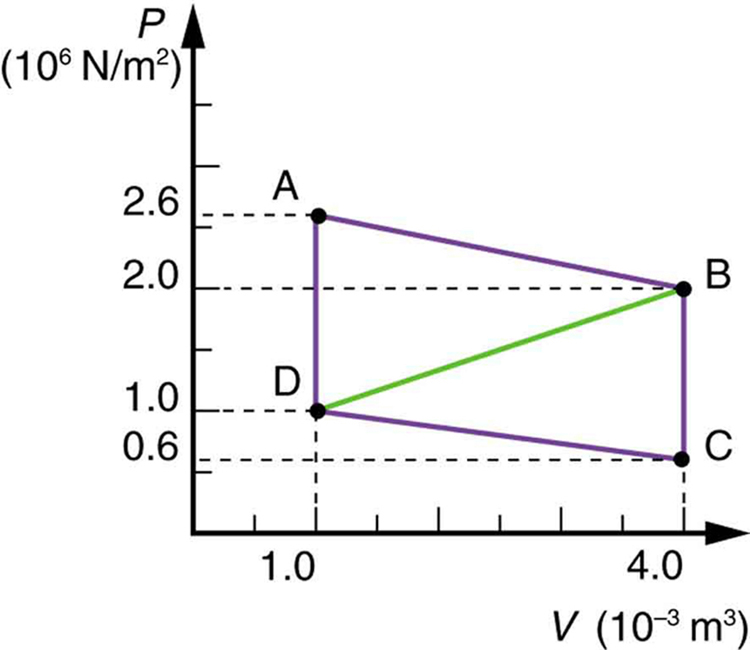
What is the net work output of a heat engine that follows path ABDA in the figure above, with a straight line from B to D? Why is the work output less than for path ABCDA? Explicitly show how you follow the steps in the Problem-Solving Strategies for Thermodynamics .
Unreasonable Results
What is wrong with the claim that a cyclical heat engine does 4.00 kJ of work on an input of 24.0 kJ of heat transfer while 16.0 kJ of heat transfers to the environment?
is not equal to the difference between the heat input and the heat output.
(a) A cyclical heat engine, operating between temperatures of and produces 4.00 MJ of work on a heat transfer of 5.00 MJ into the engine. How much heat transfer occurs to the environment? (b) What is unreasonable about the engine? (c) Which premise is unreasonable?
Construct Your Own Problem
Consider a car’s gasoline engine. Construct a problem in which you calculate the maximum efficiency this engine can have. Among the things to consider are the effective hot and cold reservoir temperatures. Compare your calculated efficiency with the actual efficiency of car engines.
Construct Your Own Problem
Consider a car trip into the mountains. Construct a problem in which you calculate the overall efficiency of the car for the trip as a ratio of kinetic and potential energy gained to fuel consumed. Compare this efficiency to the thermodynamic efficiency quoted for gasoline engines and discuss why the thermodynamic efficiency is so much greater. Among the factors to be considered are the gain in altitude and speed, the mass of the car, the distance traveled, and typical fuel economy.

Notification Switch
Would you like to follow the 'Physics 101' conversation and receive update notifications?