| << Chapter < Page | Chapter >> Page > |
The line is:
is proportional to the variance abut the line and is proportional to the variance about the line. iff the variances about both are the same.
Suppose the joint density for is constant on the unit circle about the origin. By the rectangle test, the pair cannot be independent. By symmetry, the line is and the line is . By symmetry, also, the variance about each of these lines is the same. Thus , which is true iff . This fact can be verified by calculation, if desired.
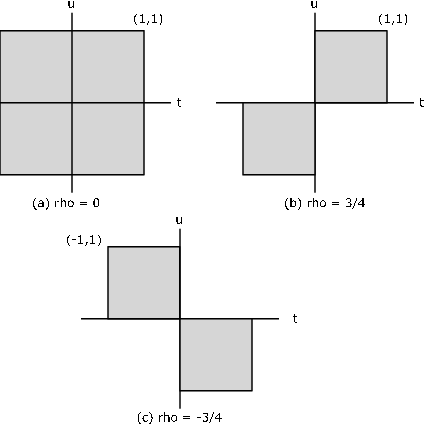
Consider the three distributions in [link] . In case (a), the distribution is uniform over the square centered at the origin with vertices at (1,1), (-1,1), (-1,-1),(1,-1). In case (b), the distribution is uniform over two squares, in the first and third quadrants with vertices (0,0), (1,0), (1,1), (0,1) and (0,0),
(-1,0), (-1,-1), (0,-1). In case (c) the two squares are in the second and fourth quadrants. The marginalsare uniform on (-1,1) in each case, so that in each case
This means the line is and the line is .
With the aid of m-functions and MATLAB we can easily caluclate the covariance and the correlation coefficient. We use the joint distribution for Example 9 in "Variance." In that example calculations show
so that .
The pair has joint density function on the triangular region bounded by , and . By the usual integration techniques, we have
From this we obtain , and . To complete the picture we need
Then
APPROXIMATION
tuappr
Enter matrix [a b]of X-range endpoints [0 1]
Enter matrix [c d]of Y-range endpoints [0 1]
Enter number of X approximation points 200Enter number of Y approximation points 200
Enter expression for joint density (6/5)*(t + 2*u).*(u>=t)
Use array operations on X, Y, PX, PY, t, u, and PEX = total(t.*P)
EX = 0.4012 % Theoretical = 0.4EY = total(u.*P)
EY = 0.7496 % Theoretical = 0.75VX = total(t.^2.*P) - EX^2
VX = 0.0603 % Theoretical = 0.06VY = total(u.^2.*P) - EY^2
VY = 0.0376 % Theoretical = 0.0375CV = total(t.*u.*P) - EX*EY
CV = 0.0201 % Theoretical = 0.02rho = CV/sqrt(VX*VY)
rho = 0.4212 % Theoretical = 0.4216 Coefficient of linear correlation
The parameter ρ is usually called the correlation coefficient. A more descriptive name would be coefficient of linear correlation . The following example shows that all probability mass may be on a curve, so that (i.e., the value of Y is completely determined by the value of X ), yet .
Suppose uniform (-1,1), so that and . Let . Then
Thus . Note that g could be any even function defined on (-1,1). In this case the integrand is odd, so that the value of the integral is zero.
Variance and covariance for linear combinations
We generalize the property (V4) on linear combinations. Consider the linear combinations
We wish to determine and . It is convenient to work with the centered random variables and . Since by linearity of expectation,
we have
and similarly for Y ' . By definition
In particular
Using the fact that , we have
Note that a i 2 does not depend upon the sign of a i . If the X i form an independent class, or are otherwise uncorrelated, the expression for variance reduces to

Notification Switch
Would you like to follow the 'Applied probability' conversation and receive update notifications?