| << Chapter < Page | Chapter >> Page > |
Having examined solving equations using the addition/subtraction and the multiplication/division principles of equality, we can combine these techniques to solve more complicated equations.
When beginning to solve an equation such as , it is helpful to know which property of equality to use first, addition/subtraction or multiplication/division. Recalling that in equation solving we are trying to isolate the variable (disassociate numbers from it), it is helpful to note the following.
To associate numbers and letters, we use the order of operations.
To undo an association between numbers and letters, we use the order of operations in reverse.
Solve each equation. (In these example problems, we will not show the checks.)
-4 is associated with
by subtraction. Undo the association by
adding 4 to
both sides.
6 is associated with
by multiplication. Undo the association by
dividing both sides by 6
3 is associated with
by addition. Undo the association by
subtracting 3 from
both sides.
-8 is associated with
by multiplication. Undo the association by
dividing both sides by -8.
Begin by solving this equation by combining like terms.
Choose a side on which to isolate
m . Since 7 is greater than 1, we'll isolate
m on the right side.
Subtract
m from
both sides.
8 is associated with
m by subtraction. Undo the association by
adding 8 to
both sides.
6 is associated with m by multiplication. Undo the association by
dividing both sides by 6.
Reduce.
Notice that if we had chosen to isolate m on the left side of the equation rather than the right side, we would have proceeded as follows:
Subtract
from
both sides.
Add 6 to
both sides,
Divide
both sides by -6.
This is the same result as with the previous approach.
7 is associated with
by division. Undo the association by
multiplying both sides by 7.
8 is associated with
by multiplication. Undo the association by
dividing both sides by 8.
Solve each equation. Be sure to check each solution.
Solve each equation. Be sure to check each result.
( [link] ) Approximating by 3.14, find the approximate circumference of the circle.
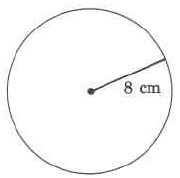
( [link] ) Find the value of .

Notification Switch
Would you like to follow the 'Fundamentals of mathematics' conversation and receive update notifications?