| << Chapter < Page | Chapter >> Page > |
Before you get started, take this readiness quiz.
In Use the Rectangular Coordinate System , we found a few solutions to the equation . They are listed in the table below. So, the ordered pairs , , , , are some solutions to the equation . We can plot these solutions in the rectangular coordinate system as shown on the graph at right.
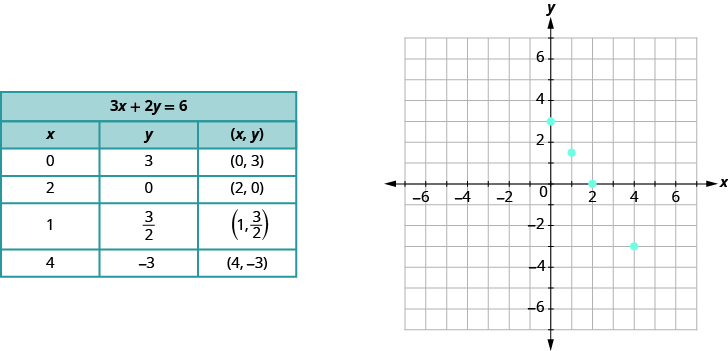
Notice how the points line up perfectly? We connect the points with a straight line to get the graph of the equation . Notice the arrows on the ends of each side of the line. These arrows indicate the line continues.
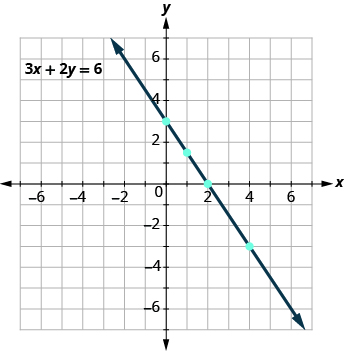
Every point on the line is a solution of the equation. Also, every solution of this equation is a point on this line. Points not on the line are not solutions!
Notice that the point whose coordinates are is on the line shown in [link] . If you substitute and into the equation, you find that it is a solution to the equation.
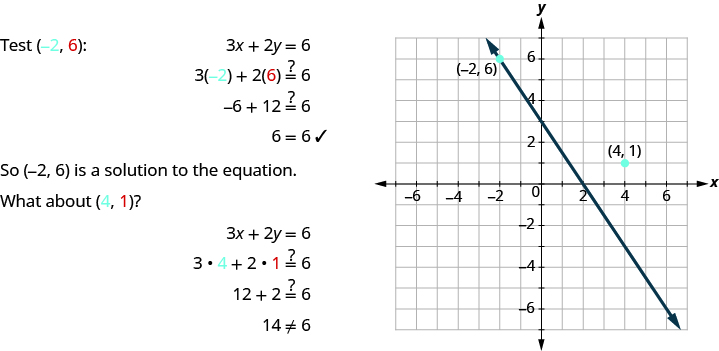
So is not a solution to the equation . Therefore the point is not on the line.
This is an example of the saying,” A picture is worth a thousand words.” The line shows you all the solutions to the equation. Every point on the line is a solution of the equation. And, every solution of this equation is on this line. This line is called the graph of the equation .
The graph of is shown below.
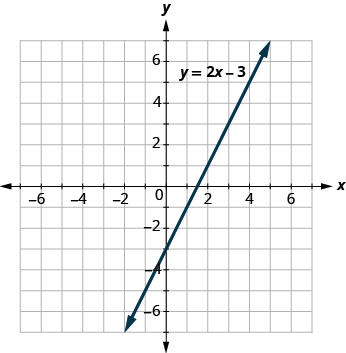
For each ordered pair decide
Substitute the - and -values into the equation to check if the ordered pair is a solution to the equation.
ⓐ

ⓑ Plot the points A:
B:
C:
and D:
.
The points
,
, and
are on the line
, and the point
is not on the line.
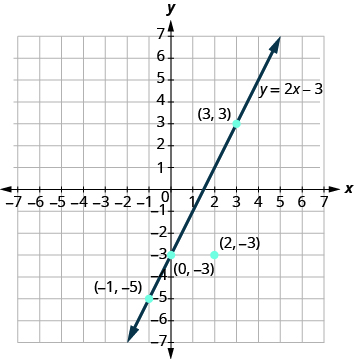
The points which are solutions to are on the line, but the point which is not a solution is not on the line.
The graph of is shown.
For each ordered pair, decide
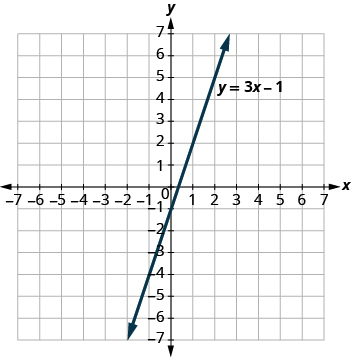
There are several methods that can be used to graph a linear equation. The method we used at the start of this section to graph is called plotting points, or the Point-Plotting Method .
Let’s graph the equation by plotting points.

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?