| << Chapter < Page | Chapter >> Page > |
Before you get started, take this readiness quiz.
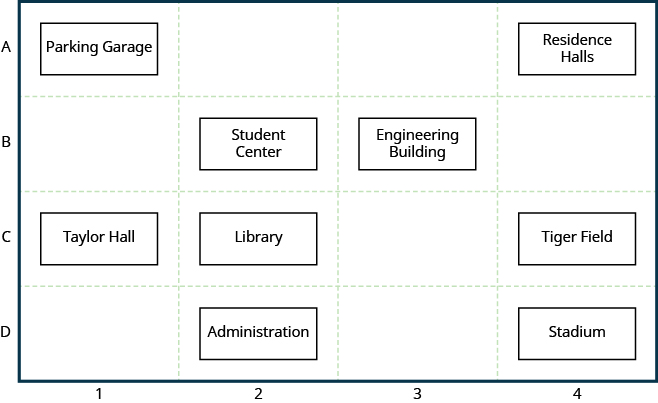
Many maps, such as the Campus Map shown in [link] , use a grid system to identify locations. Do you see the numbers and across the top and bottom of the map and the letters A, B, C, and D along the sides? Every location on the map can be identified by a number and a letter.
For example, the Student Center is in section 2B. It is located in the grid section above the number and next to the letter B. In which grid section is the Stadium? The Stadium is in section 4D.
Use the map in [link] .
Use the map in [link] .
Use the map in [link] .
Just as maps use a grid system to identify locations, a grid system is used in algebra to show a relationship between two variables in a rectangular coordinate system. To create a rectangular coordinate system, start with a horizontal number line. Show both positive and negative numbers as you did before, using a convenient scale unit. This horizontal number line is called the x -axis .
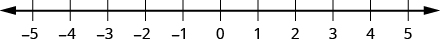
Now, make a vertical number line passing through the at Put the positive numbers above and the negative numbers below See [link] . This vertical line is called the y -axis .
Vertical grid lines pass through the integers marked on the Horizontal grid lines pass through the integers marked on the The resulting grid is the rectangular coordinate system.
The rectangular coordinate system is also called the plane, the coordinate plane, or the Cartesian coordinate system (since it was developed by a mathematician named René Descartes.)

The and the form the rectangular coordinate system. These axes divide a plane into four areas, called quadrants . The quadrants are identified by Roman numerals, beginning on the upper right and proceeding counterclockwise. See [link] .

In the rectangular coordinate system, every point is represented by an ordered pair . The first number in the ordered pair is the x -coordinate of the point, and the second number is the y -coordinate of the point.

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?