10.5 There and back again - an exploration of the liouville  (Page 5/10)

In solving the initial-value problem described in "Changing From Potential to Density" , uniqueness concerns pose the question,"Does a single Sturm-Liouville potential give rise to a single mass density?" As it turns out, no. We see that a single Sturm-Liouville potential can give rise to a set of mass densities, dependent upon the initial conditions $\rho \left(0\right)$ and ${\rho }^{\text{'}}\left(0\right)$ and the length of the recovered string, $L$ . [link] shows a color mapping of recovered string length against various initial conditions. The length of the string cannot be known before the initial-value problem is solved; therefore, in order to obtain these color maps, we fix the initial conditions and obtain the length of the string at the end of the change of variables computation. All string lengths $L\ge 1.25$ are indicated on the map as 1.25. We show this result for the transformation of three potential functions, those defined by the aforementioned spectra with ${\mu }_1=1,9,15$ . In our case, we desire strings of length one.The curve shown in black on the color maps indicates the set of initial conditions $\rho \left(0\right)$ and ${\rho }^{\text{'}}\left(0\right)$ that yield a string of unit length. Alongside this module, in the featured links, we have posted a movie of this color map with ${\mu }_1$ changing from 1 to 15 by 0.1007.

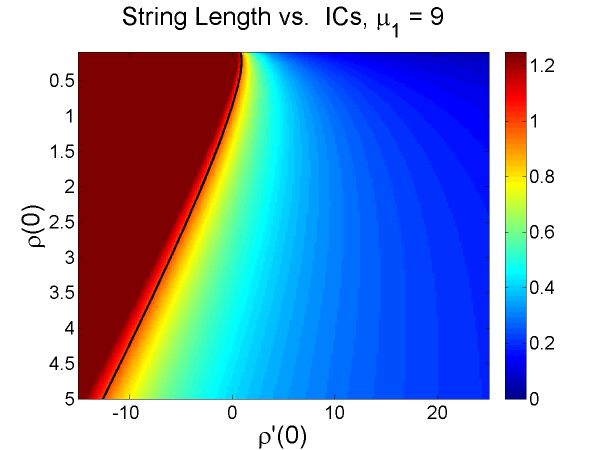
We can determine, from the curve in the color plot, a ${\rho }^{\text{'}}\left(0\right)$ corresponding to any $\rho \left(0\right)$ that will yield a string with $L=1$ for a given ${\mu }_1$ . However, we do not use this means. Instead, we choose $\rho \left(0\right)$ and use a bisection algorithm, solving the ODE at each iteration, to find ${\rho }^{\text{'}}\left(0\right)$ such that $L=1$ . The bisection algorithm is consistently called with error tolerance $\tau ={10}^{-10}$ . In the results below, we set $\rho \left(0\right)=1$ for each ${\mu }_1$ -determined potential. [link] shows the mass density functions found in this way, which correspond to the Sturm-Liouville potentials of [link] . We have also included a movie in the featured links that shows the mass density with $\rho \left(0\right)=1$ and $L=1$ from potentials determined by ${\mu }_1$ changing from 1 to 37.4 by tenths. (The second eigenvalue in the Dirichlet spectrum for [link] is $4{\pi }^2\approx 39.5$ . The closer we make ${\mu }_1$ to the second eigenvalue, the harder it is to numerically compute the transformations. Making ${\mu }_1=37.4$ was as close to $4{\pi }^2$ as we were able to compute the transformations.)

It is also interesting to view a sampling of the isospectral set of mass densities corresponding to a given $q\left(t\right)$ . Figures   [link] and   [link] contain four isospectral mass densities, each corresponding to the Sturm-Liouville potential in [link] with ${\mu }_1$ specified as in the other figures and varying values of $\rho \left(0\right)$ .

We have made the claim that the eigenvalues of the Sturm-Liouville operator specified by $q\left(t\right)$ are the same as those of the wave equation specified by the corresponding $\rho \left(x\right)$ . To demonstrate this, we consider the eigenvalue problem in   [link] . The eigenpairs can be numerically obtained via spectral methods. We build a differential matrix, $D$ , over a Chebyshev discretization of the interval and in MATLAB solve the linear system: