10.3 Short-time fourier transform

We saw earlier that Fourier analysis is not well suited to describing local changes in "frequency content" because thefrequency components defined by the Fourier transform have infinite ( i.e. , global) time support. For example, if we have a signal with periodic components plus aglitch at time $t_0$ , we might want accurate knowledge of both the periodic component frequencies and the glitch time ( [link] ).

The Short-Time Fourier Transform (STFT) provides a means of joint time-frequency analysis. The STFT pair can be written $$X_{\mathrm{STFT}}(\Omega , \tau )=\int_{()} \,d t$$∞ ∞ x t w t τ Ω t $$x(t)=\frac{1}{2\pi }\int_{()} \,d t$$∞ ∞ Ω ∞ ∞ X STFT Ω τ w t τ Ω t assuming real-valued $w(t)$ for which $\int \left|w(t)\right|^2\,d t=1$ . The STFT can be interpreted as a "sliding window CTFT": to calculate $X_{\mathrm{STFT}}(\Omega , \tau )$ , slide the center of window $w(t)$ to time $\tau$ , window the input signal, and compute the CTFT of the result ( [link] ).

"sliding window ctft"

The idea is to isolate the signal in the vicinity of time $\tau$ , then perform a CTFT analysis in order to estimate the "local" frequency content attime $\tau$ .

Essentially, the STFT uses the basis elements $$b_{\Omega ,\tau }(t)=w(t-\tau )e^{i\Omega t}$$ over the range $t\in \left\{()\right\}$∞ ∞ and $\Omega \in \left\{()\right\}$∞ ∞ . This can be understood as time and frequency shifts of the window function $w(t)$ . The STFT basis is often illustrated by a tiling of the time-frequency plane, where each tile represents aparticular basis element ( [link] ):

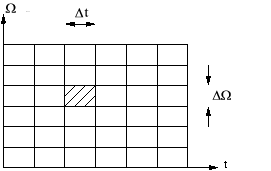
The height and width of a tile represent the spectral and temporal widths of the basis element, respectively, and theposition of a tile represents the spectral and temporal centers of the basis element. Note that, while the tiling diagram suggests that the STFT uses a discrete set of time/frequency shifts, the STFT basis is really constructed froma continuum of time/frequency shifts.

Note that we can decrease spectral width ${\Delta }_{\Omega }$ at the cost of increased temporal width ${\Delta }_t$ by stretching basis waveforms in time, although the time-bandwidth product ${\Delta }_t{\Delta }_{\Omega }$ ( i.e. , the area of each tile) will remain constant ( [link] ).

Our observations can be summarized as follows:

• the time resolutions and frequency resolutions of every STFT basis element will equal those of the window $w(t)$ . (All STFT tiles have the same shape.)
• the use of a wide window will give good frequency resolution but poor time resolution, while the use of a narrow windowwill give good time resolution but poor frequency resolution. (When tiles are stretched in one direction theyshrink in the other.)
• The combined time-frequency resolution of the basis, proportional to $\frac{1}{{\Delta }_t{\Delta }_{\Omega }}$ , is determined not by window width but by window shape. Of all shapes, the Gaussian The STFT using a Gaussian window is known as the Gabor Transform (1946). $w(t)=\frac{1}{\sqrt{2\pi }}e^{-(\frac{1}{2}t^2)}$ gives the highest time-frequency resolution, although its infinite time-support makes it impossible toimplement. (The Gaussian window results in tiles with minimum area.)