| << Chapter < Page | Chapter >> Page > |
Statistics students believe that the mean score on the first statistics test is 65. A statistics instructor thinks the mean score is higher than 65.He samples ten statistics students and obtains the scores
Set up the Hypothesis Test:
A 5% level of significance means that . This is a test of a single population mean .
: :
Since the instructor thinks the average score is higher, use a " ". The " " means the test is right-tailed.
Determine the distribution needed:
Random variable: = average score on the first statistics test.
Distribution for the test: If you read the problem carefully, you will notice that there is no population standard deviation given . You are only given sample data values. Notice also that the data come from a normal distribution. This means that thedistribution for the test is a student's-t.
Use . Therefore, the distribution for the test is where and .
Calculate the p-value using the Student's-t distribution:
) where the sample mean and sample standard deviation are calculated as 67 and 3.1972 from the data.
Interpretation of the p-value: If the null hypothesis is true, then there is a 0.0396 probability (3.96%) that the sample mean is 67 or more.

Compare and the p-value:
Since and . Therefore, .
Make a decision: Since , reject .
This means you reject . In other words, you believe the average test score is more than 65.
Conclusion: At a 5% level of significance, the sample data show sufficient evidence that the mean (average) test score is more than 65, just as the math instructor thinks.
The p-value can easily be calculated using the TI-83+ and the TI-84 calculators:
Put the data into a list. Press
STAT and arrow over to
TESTS . Press
2:T-Test . Arrow over to
Data and press
ENTER . Arrow down
and enter 65 for
, the name of the list where you put the data, and 1 for
Freq: .
Arrow down to
and arrow over to
.
Press
ENTER . Arrow down to
Calculate and press
ENTER . The calculator not
only calculates the p-value (
) but it also calculates the test statistic
(t-score) for the sample mean, the sample mean, and the sample standarddeviation.
is the alternate hypothesis. Do this set of instructions again
except arrow to
Draw (instead of
Calculate ). Press
ENTER . A shaded graph
appears with
(test statistic) and
(p-value). Make sure
when you use
Draw that no other equations are highlighted in
and the plots
are turned off.
Joon believes that 50% of first-time brides in the United States are younger than their grooms. She performs a hypothesis test to determine if the percentageis the same or different from 50% . Joon samples 100 first-time brides and 53 reply that they are younger than their grooms. For the hypothesis test, she uses a 1% level ofsignificance.
Set up the Hypothesis Test:
The 1% level of significance means that . This is a test of a single population proportion .
: :
The words "is the same or different from" tell you this is a two-tailed test.
Calculate the distribution needed:
Random variable: = the percent of of first-time brides who are younger than their grooms.
Distribution for the test: The problem contains no mention of a mean. The information is given in terms of percentages. Use the distribution for , the estimated proportion.
~ Therefore, ~ where , , and .
Calculate the p-value using the normal distribution for proportions:
or )
where , .
Interpretation of the p-value: If the null hypothesis is true, there is 0.5485 probability (54.85%) that the sample (estimated) proportion is 0.53 or more OR 0.47 or less (see the graph below).
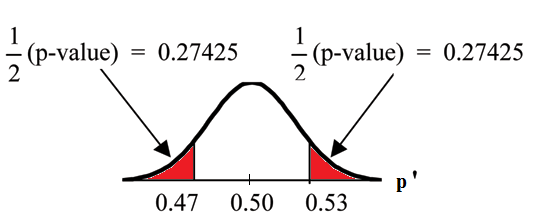
comes from , the null hypothesis.
. Since the curve is symmetrical andthe test is two-tailed, the for the left tail is equal to where . (0.03 is the differencebetween 0.53 and 0.50.)
Compare and the p-value:
Since and . Therefore, .
Make a decision: Since , you cannot reject .
Conclusion: At the 1% level of significance, the sample data do not show sufficient evidence that the percentage of first-time brides that are younger than their grooms isdifferent from 50%.
The p-value can easily be calculated using the TI-83+ and the TI-84 calculators:
Press
STAT and arrow over to
TESTS . Press
5:1-PropZTest .
Enter .5 for
,
53 for
and 100 for
. Arrow down to
Prop and arrow to
not equals
.
Press
ENTER . Arrow down to
Calculate and press
ENTER . The calculator
calculates the p-value (
) and the test statistic (z-score).
Prop not
equals .5 is the alternate hypothesis. Do this set of instructions again except
arrow to
Draw (instead of
Calculate ). Press
ENTER . A shaded graph appears
with
(test statistic) and
(p-value). Make sure when you use
Draw that no other equations are highlighted in
and the plots are turned off.
The Type I and Type II errors are as follows:
The Type I error is to conclude that the proportion of first-time brides that are younger than their grooms is different from 50% when, in fact, the proportion is actually 50%.(Reject the null hypothesis when the null hypothesis is true).
The Type II error is there is not enough evidence to conclude that the proportion of first time brides that are younger than their grooms differs from 50% when, in fact, the proportion does differ from 50%. (Do not reject the null hypothesis when the null hypothesis is false.)

Notification Switch
Would you like to follow the 'Elementary statistics' conversation and receive update notifications?