| << Chapter < Page | Chapter >> Page > |
What makes Hilbert spaces so useful in signal processing? In modern signal processing, we often represent a signal as a point in high-dimensional space. Hilbert spaces are spaces in which our geometry intuition from is most trustworthy. As an example, we will consider the approximation problem.
Let be a nonempty, closed (complete), convex set in a Hilbert space . For any there is a unique point in that is closest to , i.e., has a unique “best approximation” in .
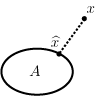
Note that in non-Hilbert spaces, this may not be true! The proof is rather technical. See Young Chapter 3 or Moon and Stirling Chapter 2 . Also known as the “closest point property”, this is very useful in compression and denoising.

Notification Switch
Would you like to follow the 'Digital signal processing' conversation and receive update notifications?