| << Chapter < Page | Chapter >> Page > |
For the following exercises, use cofunctions of complementary angles.
For the following exercises, find the lengths of the missing sides if side is opposite angle side is opposite angle and side is the hypotenuse.
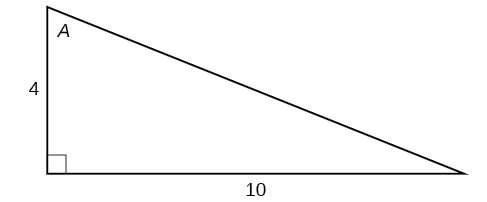
For the following exercises, use [link] to evaluate each trigonometric function of angle
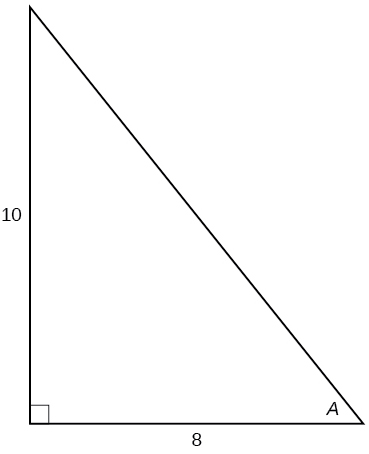
For the following exercises, use [link] to evaluate each trigonometric function of angle
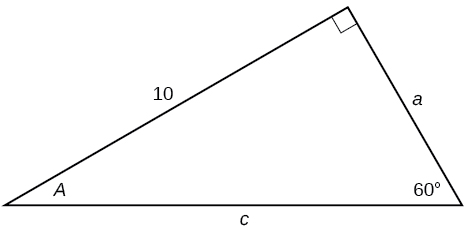
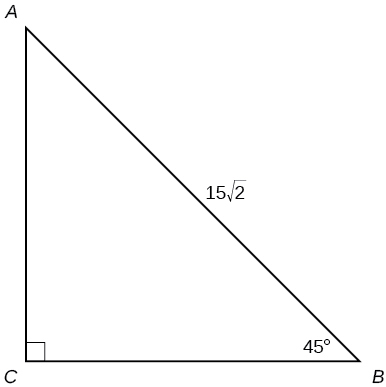
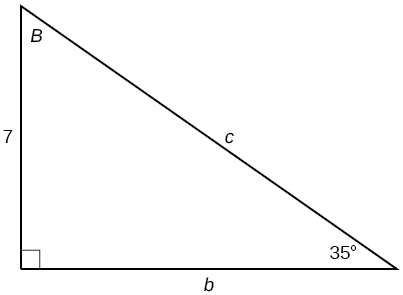
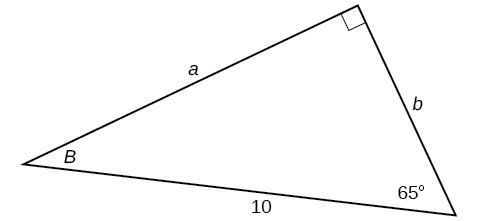
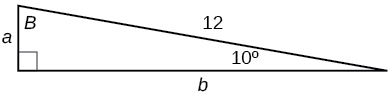
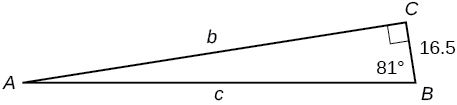
For the following exercises, solve for the unknown sides of the given triangle.

For the following exercises, use a calculator to find the length of each side to four decimal places.

Find
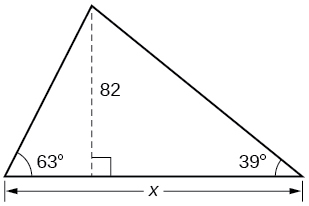
Find
188.3159
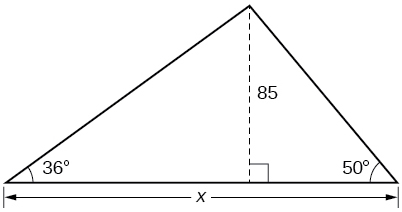
Find
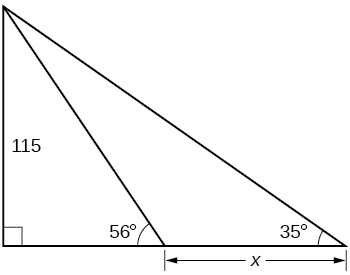
Find

200.6737
A radio tower is located 400 feet from a building. From a window in the building, a person determines that the angle of elevation to the top of the tower is and that the angle of depression to the bottom of the tower is How tall is the tower?
A radio tower is located 325 feet from a building. From a window in the building, a person determines that the angle of elevation to the top of the tower is and that the angle of depression to the bottom of the tower is How tall is the tower?
498.3471 ft
A 200-foot tall monument is located in the distance. From a window in a building, a person determines that the angle of elevation to the top of the monument is and that the angle of depression to the bottom of the tower is How far is the person from the monument?
A 400-foot tall monument is located in the distance. From a window in a building, a person determines that the angle of elevation to the top of the monument is and that the angle of depression to the bottom of the tower is How far is the person from the monument?
1060.09 ft
There is an antenna on the top of a building. From a location 300 feet from the base of the building, the angle of elevation to the top of the building is measured to be From the same location, the angle of elevation to the top of the antenna is measured to be Find the height of the antenna.
There is lightning rod on the top of a building. From a location 500 feet from the base of the building, the angle of elevation to the top of the building is measured to be From the same location, the angle of elevation to the top of the lightning rod is measured to be Find the height of the lightning rod.
27.372 ft
A 33-ft ladder leans against a building so that the angle between the ground and the ladder is How high does the ladder reach up the side of the building?

Notification Switch
Would you like to follow the 'Essential precalculus, part 2' conversation and receive update notifications?