1.3 Normed vector spaces

While vector spaces have additional structure compared to a metric space, a general vector space has no notion of “length” or “distance.”

Definition 1

• N1. $∥x∥\ge 0\forall x\in V$
• N2. $∥x∥=0$ iff $x=0$
• N3. $∥\alpha ,x∥=\left|\alpha \right|∥x∥\forall x\in V$ , $\alpha \in K$
• N4. $∥x,+,y∥\le ∥x∥+∥y∥\forall x,y\in V$

A vector space together with a norm is called a normed vector space (or normed linear space ).

Note that any normed vector space is a metric space with induced metric $d(x,y)=∥x,-,y∥$ . (This follows since $∥x,-,y∥=∥x,-,z,+,z,-,y∥\in ∥x,-,z∥+∥y,-,z∥$ .) While a normed vector space “feels like” a metric space, it is important to remember that it actually satisfies a great deal of additional structure.

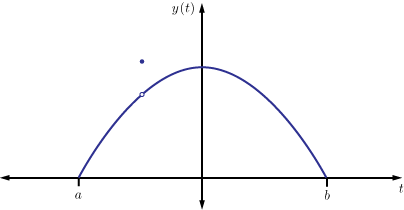
Technical Note: In a normed vector space we must have (from N2) that $x=y$ if $∥x,-,y∥=0$ . This can lead to a curious phenomenon when dealing with continuous-time functions. For example, in $L_2\left([a,b]\right)$ , we can consider a pair of functions like $x\left(t\right)$ and $y\left(t\right)$ illustrated below. These functions differ only at a single point, and thus ${\parallel x\left(t\right)-y\left(t\right)\parallel }_2=0$ (since a single point cannot contribute anything to the value of the integral.) Thus, in order for our norm to be consistent with the axioms of a norm, we must say that $x=y$ whenever $x\left(t\right)$ and $y\left(t\right)$ differ only on a set of measure zero. To reiterate $x=y\nLeftrightarrow x\left(t\right)=y\left(t\right)\forall t\in [a,b]$ , i.e., when we treat functions as vectors, we will not interpret $x=y$ as pointwise equality, but rather as equality almost everywhere .