| << Chapter < Page | Chapter >> Page > |
Up to Grade 2 the learners used the word “ones” for “units” but as from Grade 3 we change to “units”. Explain it to the learners.
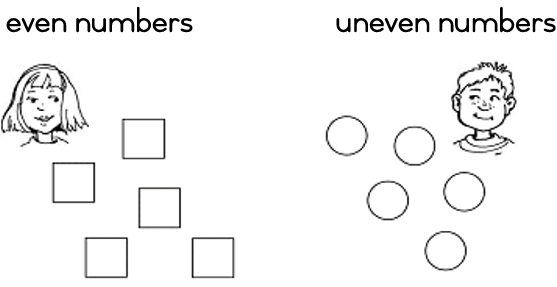
Use concrete objects and help the learners to discover for themselves what even and uneven numbers are. Do this to 9 at first.
Help them to discover the pattern from 11 to 19.
When they have discovered the pattern of 2 4 6 8 0 on the unit side for even numbers and 1 3 5 7 9 on the unit side for uneven numbers, they have fun applying this to higher numbers.

All the SQUARES belong to Bonny. She has all the numbers with a 2 ................... ................... ................... 0 on the side of the ones (units). All her numbers are therefore even numbers.
All the CIRCLES belong to Tommy. He has all the numbers with a
1 ................. ................. ................. ................. on the side of the ones (units). All his numbers are therefore uneven numbers.
23 38 14 9 56 80 75 2 61 97
| LO 1.4 | LO 2.2 |

| LO 1.9 |


| LO 1.8 |
Learning Outcome 1: The learner will be able to recognise, describe and represent numbers and their relationships, and to count, estimate, calculate and check with competence and confidence in solving problems.
Assessment Standard 1.4: We know this when the learner orders, describes and compares the following numbers:
1.4.1 whole numbers to at least 3-digit numbers;
1.4.2 common fractions including halves, quarters and thirds;
Assessment Standard 1.8: We know this when the learner can perform calculations, using appropriate symbols, to solve problems involving:
1.8.1 addition and subtraction of whole numbers with at least 3 digits;
1.8.2 multiplication of at least whole 2-digit by 1-digit numbers;
1.8.3 division of at least whole 2-digit by 1-digit numbers;
1.8.4 estimation;
Assessment Standard 1.9: We know this when the learner performs mental calculations involving:
1.9.1 addition and subtraction for numbers to at least 50;
1.9.2 multiplication of whole numbers with solutions to at least 50.
Learning Outcome 2: The learner will be able to recognise, describe and represent patterns and relationships, as well as to solve problems using algebraic language and skills.
Assessment Standard 2.2: We know this when the learner copies and extends simple number sequences to at least 1 000.

Notification Switch
Would you like to follow the 'Mathematics grade 3' conversation and receive update notifications?