This module is from Fundamentals of Mathematics by Denny Burzynski and Wade Ellis, Jr. This module discusses how to add signed numbers. By the end of the module students should be able to add numbers with like signs and with unlike signs and be able to use the calculator for addition of signed numbers.
Section overview
- Addition of Numbers with Like Signs
- Addition with Zero
- Addition of Numbers with Unlike Signs
- Calculators
Addition of numbers with like signs
The addition of the
two positive numbers 2 and 3 is performed on the number line as follows.
Begin at 0, the origin.
Since 2 is positive, move 2 units to the right.
Since 3 is positive, move 3 more units to the right.
We are now located at 5.

Thus,
.
Summarizing, we have
The addition of the
two negative numbers -2 and -3 is performed on the number line as follows.
Begin at 0, the origin.
Since -2 is negative, move 2 units to the left.
Since -3 is negative, move 3 more units to the left.
We are now located at -5.

Thus,
.
Summarizing, we have
Observing these two examples, we can suggest these relationships:
Adding numbers with the same sign
Addition of numbers with like sign:
To add two real numbers that have the
same sign, add the absolute values of the numbers and associate with the sum the common sign.
Sample set a
Find the sums.
Add these absolute values.
The common sign is “+.”
Thus,
, or
.
Add these absolute values.
The common sign is “
.“
Thus,
.
Practice set a
Find the sums.
Addition with zero
Addition with zero
Notice that
.
.
The additive identity is zero
Since adding zero to a real number leaves that number unchanged, zero is called the
additive identity .
Addition of numbers with unlike signs
The addition
,
two numbers with unlike signs , can also be illustrated using the number line.
Begin at 0, the origin.
Since 2 is positive, move 2 units to the right.
Since -6 is negative, move, from 2, 6 units to the left.
We are now located at -4.

We can suggest a rule for adding two numbers that have
unlike signs by noting that if the signs are disregarded, 4 can be obtained by subtracting 2 from 6. But 2 and 6 are precisely the absolute values of 2 and -6. Also, notice that the sign of the number with the larger absolute value is negative and that the sign of the resulting sum is negative.
Adding numbers with unlike signs
Addition of numbers with unlike signs: To add two real numbers that have
unlike signs , subtract the smaller absolute value from the larger absolute value and associate with this difference the sign of the number with the larger absolute value.
Sample set b
Find the following sums.
Subtract absolute values:
.
Attach the proper sign: "+."
Thus,
or
.
Subtract absolute values:
.
Attach the proper sign: "
."
Thus,
.
The morning temperature on a winter's day in Lake Tahoe was -12 degrees. The afternoon temperature was 25 degrees warmer. What was the afternoon temperature?
We need to find
.
Subtract absolute values:
.
Attach the proper sign: "+."
Thus,
.
Practice set b
Find the sums.
Calculators
Calculators having the
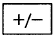 key can be used for finding sums of signed numbers.
key can be used for finding sums of signed numbers.
Sample set c
Use a calculator to find the sum of -147 and 84.
|
|
Display Reads |
|
| Type |
147 |
147 |
|
| Press |
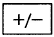 |
-147 |
This key changes the sign of a number. It is different than
. |
| Press |
+ |
-147 |
|
| Type |
84 |
84 |
|
| Press |
= |
-63 |
|
Practice set c
Use a calculator to find each sum.
Exercises
Find the sums in the following 27 problems. If possible, use a calculator to check each result.
In order for a small business to break even on a project, it must have sales of $21,000. If the amount of sales was $15,000, by how much money did this company fall short?
Suppose a person has $56 in his checking account. He deposits $100 into his checking account by using the automatic teller machine. He then writes a check for $84.50. If an error causes the deposit not to be listed into this person’s account, what is this person’s checking balance?
A person borrows $7 on Monday and then $12 on Tuesday. How much has this person borrowed?
A person borrows $11 on Monday and then pays back $8 on Tuesday. How much does this person owe?
Exercises for review
(
[link] ) Find the reciprocal of
.
(
[link] ) Find the value of
.
(
[link] ) Round 0.01628 to the nearest tenth.
(
[link] ) Convert 62% to a fraction.
(
[link] ) Find the value of
.



![]() key can be used for finding sums of signed numbers.
key can be used for finding sums of signed numbers.