1. Home
  2. Digital signal processing
  3. Signal representation and
  4. Orthogonal bases

1.15 Orthogonal bases

<< Chapter < Page
  Digital signal processing   Page 1 / 1
Chapter >> Page >

Definition 1

A collection of vectors B in an inner product space V is called an orthogonal basis if

  1. span ( B ) = V
  2. v i ⊥ v j (i.e., ⟨ v i , v j ⟩ = 0 ) ∀ i ≠ j

If, in addition, the vectors are normalized under the induced norm, i.e., ∥ v i ∥ = 1 ∀ i , then we call V an orthonormal basis (or “orthobasis” ). If V is infinite dimensional, we need to be a bit more careful with 1. Specifically, we really only need the closure of span ( B ) to equal V . In this case any x ∈ V can be written as

x = ∑ i = 1 ∞ c i v i

for some sequence of coefficients { c i } i = 1 ∞ .

(This last point is a technical one since the span is typically defined as the set of linear combinations of a finite number of vectors. See Young Ch 3 and 4 for the details. This won't affect too much so we will gloss over the details.)

  • V = R 2 , standard basis
    v 1 = 1 0 v 2 = 0 1
  • Suppose V = { piecewise constant functions on [ 0 , 1 4 ) , [ 1 4 , 1 2 ) , [ 1 2 , 3 4 ) , [ 3 4 , 1 ] } . An example of such a function is illustrated below.
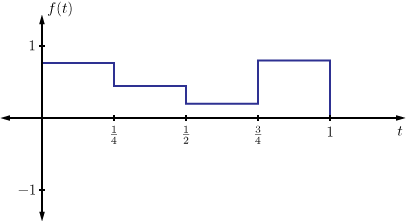
    An example of a piecewise constant function.
    Consider the set
    Illustrations of the Haar basis functions. v_1 is the all constant function, i.e., it is 1 on [0,1]. Illustrations of the Haar basis functions. v_2 is 1 on [0,0.5) and -1 on [0.5,1]. Illustrations of the Haar basis functions. v_3 is sqrt(2) on [0,0.25), -sqrt(2) on [0.25,0.5), and 0 on [0.5,1]. Illustrations of the Haar basis functions. v_4 is 0 on [0,0.5), sqrt(2) on [0.5,0.75), and -sqrt(2) on [0.75,1].
    The vectors { v 1 , v 2 , v 3 , v 4 } form an orthobasis for V .
  • Suppose V = L 2 [ - π , π ] . B = { 1 2 π e j k t } k = - ∞ ∞ , i.e, the Fourier series basis vectors, form an orthobasis for V . To verify the orthogonality of the vectors, note that:
    1 2 π e j k t , 1 2 π e j k t = 1 2 π ∫ - π π e j ( k 1 - k 2 ) t = 1 2 π e j ( k 1 - k 2 ) t j ( k 1 - k 2 ) - π π = 1 2 π · - 1 + 1 j ( k 1 - k 2 ) = 0 ( k 1 ≠ k 2 )
    See Young for proof that the closure of B is L 2 [ - π , π ] , i.e., the fact that any f ∈ L 2 [ - π , π ] has a Fourier series representation.
<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Digital signal processing. OpenStax CNX. Dec 16, 2011 Download for free at http://cnx.org/content/col11172/1.4
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Digital signal processing' conversation and receive update notifications?

Ask