This module offers a brief and generally intuitive introduction to maximum likelihood estimation methods. It is intended as a guide for advanced undergraduates.
The maximum likelihood method
Introduction
The maximum likelihood (ML) method is an alternative to ordinary least squares (OLS) and offers a more general approach to the problem of finding estimators of unknown population parameters. In these notes we present an intuitive introduction to the ML technique. We begin our discussion with a description of continuous random variables.
Continuous random variables
Assume that
x
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaaaa@36F1@ is a continuous random variable over the interval
−
∞
≤
x
≤
∞
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyOeI0IaeyOhIuQaeyizImQaamiEaiabgsMiJkabg6HiLkaac6caaaa@3EDC@ Because of the assumption of continuity we need some special definitions.
Probability density function . Any function
f
(
x
)
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabmaabaGaamiEaaGaayjkaiaawMcaaaaa@3965@ that has the following characteristics is a probability density function (pdf): (1)
f
(
x
)
>
0
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabmaabaGaamiEaaGaayjkaiaawMcaaiabg6da+iaaicdaaaa@3B27@ and (2)
∫
−
∞
∞
f
(
x
)
d
x
=
1.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qCaeaacaWGMbWaaeWaaeaacaWG4baacaGLOaGaayzkaaGaamizaiaadIhaaSqaaiabgkHiTiabg6HiLcqaaiabg6HiLcqdcqGHRiI8aOGaeyypa0JaaGymaiaac6caaaa@4400@ The probability that
x has a value between
a and
b is given by
Pr
(
a
≤
x
≤
b
)
=
∫
a
b
f
(
x
)
d
x
.
MathType@MTEF@5@5@+=feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiuaiaackhadaqadaqaaiaadggacqGHKjYOcaWG4bGaeyizImQaamOyaaGaayjkaiaawMcaaiabg2da9maapehabaGaamOzamaabmaabaGaamiEaaGaayjkaiaawMcaaiaadsgacaWG4baaleaacaWGHbaabaGaamOyaaqdcqGHRiI8aOGaaiOlaaaa@4ACB@ Here are two examples of the probability density functions (pdf) of continuous random variables.
Let
f
(
x
)
=
1
α
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabmaabaGaamiEaaGaayjkaiaawMcaaiabg2da9maalaaabaGaaGymaaqaaiabeg7aHbaaaaa@3CD5@ for
0
≤
x
≤
α
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGimaiabgsMiJkaadIhacqGHKjYOcqaHXoqyaaa@3CB4@ and 0 elsewhere, where
α
>
0.
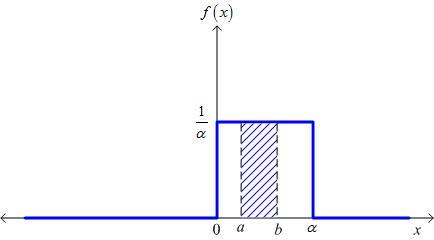
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqySdeMaeyOpa4JaaGimaiaac6caaaa@3A07@ A graph of the pdf for this distribution is shown in Figure 1.
Probability distribution function of a uniform distribution.
The probability
x falls between
a and
b is given by the colored in area.
It is easy to see from the graph that
f
(
x
)
=
1
α
>
0
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabmaabaGaamiEaaGaayjkaiaawMcaaiabg2da9maalaaabaGaaGymaaqaaiabeg7aHbaacqGH+aGpcaaIWaaaaa@3E97@ and
Pr
(
a
≤
x
≤
b
)
=
∫
−
∞
∞
f
(
x
)
d
x
=
∫
0
α
1
α
d
x
=
1.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaeiiaiaabccaciGGqbGaaiOCamaabmaabaGaamyyaiabgsMiJkaadIhacqGHKjYOcaWGIbaacaGLOaGaayzkaaGaeyypa0Zaa8qCaeaacaWGMbWaaeWaaeaacaWG4baacaGLOaGaayzkaaGaamizaiaadIhaaSqaaiabgkHiTiabg6HiLcqaaiabg6HiLcqdcqGHRiI8aOGaeyypa0Zaa8qCaeaadaWcaaqaaiaaigdaaeaacqaHXoqyaaGaamizaiaadIhaaSqaaiaaicdaaeaacqaHXoqya0Gaey4kIipakiabg2da9iaaigdacaGGUaaaaa@59F7@ Moreover, as shown in Figure 1, the area under the pdf curve between
a and
b is equal to the probability that
x lies between
a and
b ; that is,
Pr
(
a
≤
x
≤
b
)
=
∫
a
b
(
1
α
)
d
x
=
x
α
|
a
b
=
b
−
a
α
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiuaiaackhadaqadaqaaiaadggacqGHKjYOcaWG4bGaeyizImQaamOyaaGaayjkaiaawMcaaiabg2da9maapehabaWaaeWaaeaadaWcaaqaaiaaigdaaeaacqaHXoqyaaaacaGLOaGaayzkaaGaamizaiaadIhaaSqaaiaadggaaeaacaWGIbaaniabgUIiYdGccqGH9aqpdaabcaqaamaalaaabaGaamiEaaqaaiabeg7aHbaaaiaawIa7amaaDaaaleaacaWGHbaabaGaamOyaaaakiabg2da9maalaaabaGaamOyaiabgkHiTiaadggaaeaacqaHXoqyaaGaaiOlaaaa@5809@
The calculation of the mean and variance of this distribution is relatively simple. The population mean is given by
μ
x
=
E
(
x
)
=
∫
0
α
x
f
(
x
)
d
x
MathType@MTEF@5@5@+=feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiVd02aaSbaaSqaaiaadIhaaeqaaOGaeyypa0JaamyramaabmaabaGaamiEaaGaayjkaiaawMcaaiabg2da9maapehabaGaamiEaiaadAgadaqadaqaaiaadIhaaiaawIcacaGLPaaacaWGKbGaamiEaaWcbaGaaGimaaqaaiabeg7aHbqdcqGHRiI8aaaa@494E@ or
μ
x
=
∫
0
α
x
(
1
α
)
d
x
=
x
2
2
α
|
0
α
=
α
2
.
MathType@MTEF@5@5@+=feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiVd02aaSbaaSqaaiaadIhaaeqaaOGaeyypa0Zaa8qCaeaacaWG4bWaaeWaaeaadaWcaaqaaiaaigdaaeaacqaHXoqyaaaacaGLOaGaayzkaaGaamizaiaadIhaaSqaaiaaicdaaeaacqaHXoqya0Gaey4kIipakiabg2da9maaeiaabaWaaSaaaeaacaWG4bWaaWbaaSqabeaacaaIYaaaaaGcbaGaaGOmaiabeg7aHbaaaiaawIa7amaaDaaaleaacaaIWaaabaGaeqySdegaaOGaeyypa0ZaaSaaaeaacqaHXoqyaeaacaaIYaaaaaaa@527C@
The population variance
is given by
V
(
x
)
=
E
[
(
x
−
μ
x
)
2
.
]
MathType@MTEF@5@5@+=feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOvamaabmaabaGaamiEaaGaayjkaiaawMcaaiabg2da9iaadweadaWadaqaamaabmaabaGaamiEaiabgkHiTiabeY7aTnaaBaaaleaacaWG4baabeaaaOGaayjkaiaawMcaamaaCaaaleqabaGaaGOmaaaaaOGaay5waiaaw2faaaaa@4465@ Thus,
V
(
x
)
=
∫
0
α
(
x
−
α
2
)
2
(
1
α
)
d
x
=
∫
0
α
(
x
2
−
α
x
+
α
2
4
)
(
1
α
)
d
x
MathType@MTEF@5@5@+=feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOvamaabmaabaGaamiEaaGaayjkaiaawMcaaiabg2da9maapehabaWaaeWaaeaacaWG4bGaeyOeI0YaaSaaaeaacqaHXoqyaeaacaaIYaaaaaGaayjkaiaawMcaamaaCaaaleqabaGaaGOmaaaakmaabmaabaWaaSaaaeaacaaIXaaabaGaeqySdegaaaGaayjkaiaawMcaaiaadsgacaWG4baaleaacaaIWaaabaGaeqySdeganiabgUIiYdGccqGH9aqpdaWdXbqaamaabmaabaGaamiEamaaCaaaleqabaGaaGOmaaaakiabgkHiTiabeg7aHjaadIhacqGHRaWkdaWcaaqaaiabeg7aHnaaCaaaleqabaGaaGOmaaaaaOqaaiaaisdaaaaacaGLOaGaayzkaaWaaeWaaeaadaWcaaqaaiaaigdaaeaacqaHXoqyaaaacaGLOaGaayzkaaGaamizaiaadIhaaSqaaiaaicdaaeaacqaHXoqya0Gaey4kIipaaaa@62B5@ or
V
(
x
)
=
x
3
3
α
−
x
2
2
+
α
4
x
|
0
α
=
α
2
3
−
α
2
2
+
α
2
4
=
α
2
12
.
MathType@MTEF@5@5@+=feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOvamaabmaabaGaamiEaaGaayjkaiaawMcaaiabg2da9maaeiaabaWaaSaaaeaacaWG4bWaaWbaaSqabeaacaaIZaaaaaGcbaGaaG4maiabeg7aHbaacqGHsisldaWcaaqaaiaadIhadaahaaWcbeqaaiaaikdaaaaakeaacaaIYaaaaiabgUcaRmaalaaabaGaeqySdegabaGaaGinaaaacaWG4baacaGLiWoadaqhaaWcbaGaaGimaaqaaiabeg7aHbaakiabg2da9maalaaabaGaeqySde2aaWbaaSqabeaacaaIYaaaaaGcbaGaaG4maaaacqGHsisldaWcaaqaaiabeg7aHnaaCaaaleqabaGaaGOmaaaaaOqaaiaaikdaaaGaey4kaSYaaSaaaeaacqaHXoqydaahaaWcbeqaaiaaikdaaaaakeaacaaI0aaaaiabg2da9maalaaabaGaeqySde2aaWbaaSqabeaacaaIYaaaaaGcbaGaaGymaiaaikdaaaGaaiOlaaaa@5D95@
Because of the simple mathematical form of the uniform pdf, the calculations in Example 1 are relatively straight forward. While the calculations for random variables with a pdf that has a more complicated form are generally more difficult (if algebraically possible), the basic methodology remains the same. Example 2 considers the case of a more complicated pdf.
The normal distribution.
A random variable with a mean of
μ
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiVd0gaaa@37AA@ and a variance of
σ
2
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaaa@38A0@ that has a
normal distribution —that is,
x
~
N
(
μ
,
σ
2
)
—
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiaac6hacaWGobWaaeWaaeaacqaH8oqBcaGGSaGaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaGccaGLOaGaayzkaaGaaiifGaaa@4023@ has the pdf
f
(
x
)
=
1
σ
2
π
e
−
(
x
−
μ
)
2
2
σ
2
.
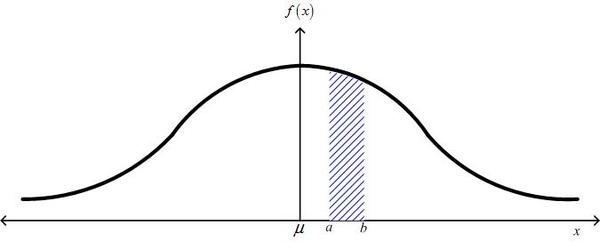
MathType@MTEF@5@5@+=feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabmaabaGaamiEaaGaayjkaiaawMcaaiabg2da9maalaaabaGaaGymaaqaaiabeo8aZnaakaaabaGaaGOmaiabec8aWbWcbeaaaaGccaWGLbWaaWbaaSqabeaacqGHsisldaWcaaqaamaabmaabaGaamiEaiabgkHiTiabeY7aTbGaayjkaiaawMcaamaaCaaameqabaGaaGOmaaaaaSqaaiaaikdacqaHdpWCdaahaaadbeqaaiaaikdaaaaaaaaakiaac6caaaa@4BED@ A typical graph of this pdf is given in Figure 2. The area under the curve between values of
x of
a and
b is equal to the probability that
x falls between
a and
b .
Probability distribution function of a normal distribution.
The probability
x falls between
a and
b is given by the shaded area.
Joint distributions of samples and the ml method.
Most of the statistical work that economists use involves the use of a sample of observations. It is usual to assume that the members of the sample are drawn independently of each other. The implication of this assumption is that
the pdf of the joint distribution is equal to the product of the pfd of each observation ; i.e.,