| << Chapter < Page | Chapter >> Page > |
Find two different sets of parametric equations to represent the graph of
One possibility is Another possibility is
There are, in fact, an infinite number of possibilities.
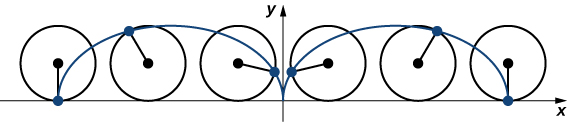
Imagine going on a bicycle ride through the country. The tires stay in contact with the road and rotate in a predictable pattern. Now suppose a very determined ant is tired after a long day and wants to get home. So he hangs onto the side of the tire and gets a free ride. The path that this ant travels down a straight road is called a cycloid ( [link] ). A cycloid generated by a circle (or bicycle wheel) of radius a is given by the parametric equations
To see why this is true, consider the path that the center of the wheel takes. The center moves along the x -axis at a constant height equal to the radius of the wheel. If the radius is a , then the coordinates of the center can be given by the equations
for any value of Next, consider the ant, which rotates around the center along a circular path. If the bicycle is moving from left to right then the wheels are rotating in a clockwise direction. A possible parameterization of the circular motion of the ant (relative to the center of the wheel) is given by
(The negative sign is needed to reverse the orientation of the curve. If the negative sign were not there, we would have to imagine the wheel rotating counterclockwise.) Adding these equations together gives the equations for the cycloid.
Now suppose that the bicycle wheel doesn’t travel along a straight road but instead moves along the inside of a larger wheel, as in [link] . In this graph, the green circle is traveling around the blue circle in a counterclockwise direction. A point on the edge of the green circle traces out the red graph, which is called a hypocycloid .
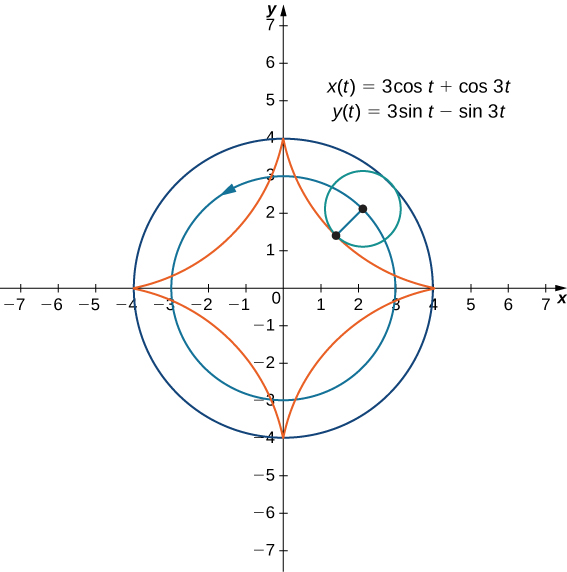
The general parametric equations for a hypocycloid are
These equations are a bit more complicated, but the derivation is somewhat similar to the equations for the cycloid. In this case we assume the radius of the larger circle is a and the radius of the smaller circle is b. Then the center of the wheel travels along a circle of radius This fact explains the first term in each equation above. The period of the second trigonometric function in both and is equal to
The ratio is related to the number of cusps on the graph (cusps are the corners or pointed ends of the graph), as illustrated in [link] . This ratio can lead to some very interesting graphs, depending on whether or not the ratio is rational. [link] corresponds to and The result is a hypocycloid with four cusps. [link] shows some other possibilities. The last two hypocycloids have irrational values for In these cases the hypocycloids have an infinite number of cusps, so they never return to their starting point. These are examples of what are known as space-filling curves .

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?