1.1 A brief introduction to computational algebraic geometry  (Page 3/20)

so that for $(x,y)=\left(x\right(t),y(t\left)\right)$ with $t$ very small,

and dividing through by $x^m$ , we get

Now, since $x\left(t\right)\to 0$ and $y\left(t\right)\to 0$ as $t\to 0^{+}$ and $y\left(t\right)/x\left(t\right)$ stays bounded, ${lim}_{t\to 0^{+}}\frac{x{\left(t\right)}^{j}y{\left(t\right)}^{m+i-j}}{x{\left(t\right)}^m}=0$ for $i>0$ and we find that

This implies that

so that the slope $c$ of the tangent line is a root of the polynomial $a_0+a_{1}z+\cdots +a_{m-1}{z}^{m-1}+a_m{z}^m$ . Equivalently, $z-c$ is a factor of $a_0+a_{1}z+\cdots +a_{m-1}{z}^{m-1}+a_m{z}^m$ and $y-cx$ is a factor of $f_m=a_0{x}^m+a_1{x}^{m-1}y+\cdots +a_{m-1}x{y}^{m-1}+a_m{y}^m$ as desired (Why?).

If we had been dealing with a vertical tangent, then we could have divided through by $y^m$ instead, and we would find that

which implies that 0 must be a root of the polynomial $a_0{w}^m+a_1{w}^{m-1}+\cdots a_{m-1}w+\cdots a_m$ so that $x$ is a factor of the polynomial $f_m=a_0{x}^m+a_1{x}^{m-1}y+\cdots +a_{m-1}x{y}^{m-1}+a_m{y}^m$ .

It turns out that, at least over the complex numbers, the converse of this proposition is true as well: if $ax+by$ is a factor of $f_m$ , then near the origin there is a branch of the curve $V\left(f\right)$ having $V(ax+by)$ as its tangent line at the origin.

We call that smallest degree $m$ of a non-zero term of $f$ the multiplicity of the curve $X=V\left(f\right)$ at the origin. Since $V\left(f_m\right)$ is often the union of the tangent lines to branches of the curve $X$ at the origin (and at least always contains those lines) we'll give it a name: we call $V\left(f_m\right)$ the tangent cone of $X$ at the origin and denote it $T{C}_{(0,0)}\left(X\right)$ .

We said that we could move a singular point of $X=V\left(f\right)$ to the origin by a change of coordinates, but we could also have done everything with Taylor expansions centered at any point $p=(a,b)$ : we set $f_k$ to be the degree $k$ part of $f$ regarded as a polynomial in $x-a$ and $y-b$ , as can be computed by Taylor expansion

We can then define the multiplicity $m$ as before as the the smallest number so that $f_m\ne 0$ , and define the tangent cone to $X$ at $p$ to be $T{C}_p\left(X\right)=V\left(f_m\right)$ . One can check that this agrees with what we'd get by instead translating the curve $X$ so that $p$ goes to the origin, computing the tangent cone at the origin as above and then translating back.

One might wonder where the term “cone” is coming from here given that there is no cone in the traditional sense in sight. The answer is that the term “cone” is often used more generally to refer to any locus traced out by lines through some fixed point (the vertex of the “cone”). Here, the “base” of the tangent cone of our plane curve might be regarded as finitely many points, one for each tangent direction. While this can never really look much like a more familiar cone in the case of plane curves, it is possible for a “tangent cone” to a singular point on a surface to actually be a “cone” in the original sense (see [link] ).

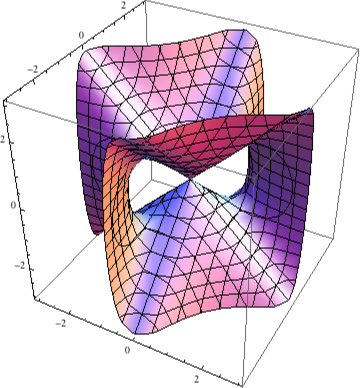
Exercise Show that if $f(x_1,...,x_n)\in \mathbf{R}[x_1,...,x_n]$ is a homogeneous polynomial (all of its terms have the same degree), then its zero locus $V\left(f\right)$ is a cone with vertex $(0,...,0)$ , i.e. if $(c_1,...,c_n)\in V\left(f\right)$ then $(\lambda c_1,...,\lambda c_n)\in V\left(f\right)$ for all $\lambda \in \mathbf{R}$ .