| << Chapter < Page | Chapter >> Page > |
The equations of motion are as follows.
The boundary conditions are zero stress at the gas-liquid interface and no slip at the wall.
The shear stress profile can be determined by integration and application of the zero stress boundary condition.
The velocity profile for a Newtonian fluid can be determined by a second integration and application of the no slip boundary condition.
The average velocity and volumetric flow rate can be determined by integration of the velocity profile over the film thickness.
The film thickness, h, can be given in terms of the average velocity, the volume rate of flow, or the mass rate of flow per unit width of wall :
Suddenly accelerated plate. (BSL, 1960) A semi-infinite body of liquid with constant density and viscosity is bounded on one side by a flat surface ( the plane). Initially the fluid and solid surface is at rest; but at time the solid surface is set in motion in the positive -direction with a velocity . It is desired to know the velocity as a function of and . The pressure is hydrostatic and the flow is assumed to be laminar.
The only nonzero component of velocity is . Thus the only non-zero equation of motion is as follows.
The initial condition and boundary conditions are as follows.
If we normalize the velocity with respect to the boundary condition, we see that this is the same parabolic PDE and boundary condition as we solved with a similarity transformation. Thus the solution is
The presence of the ratio of viscosity and density, the kinematic viscosity, in the expression for the velocity implies that both viscous and inertial forces are operative.
The velocity profiles for the wall at suddenly set in motion is illustrated below.

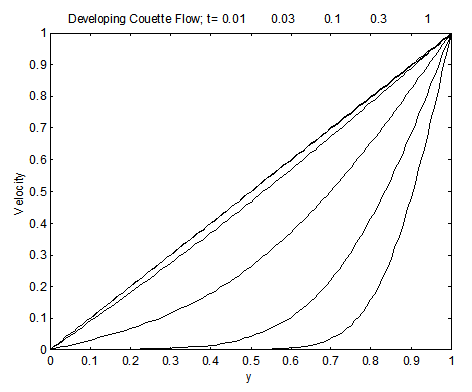
Developing Couette flow. The transient development to the steady-state Couette flow discussed earlier can now be easily derived. We will let the plane be the surface with zero velocity and let the velocity be specified at . The initial and boundary conditions are as follows.
It should be apparent that the two formulations of the boundary conditions give the same solution. However, the latter gives a clue how one should obtain a solution. The solution is antisymmetric about and the zero velocity condition is satisfied. A series of additional terms are needed to satisfy the boundary conditions at . The solution is

Notification Switch
Would you like to follow the 'Transport phenomena' conversation and receive update notifications?