0.7 Generalizations of the basic multiresolution wavelet system  (Page 25/28)

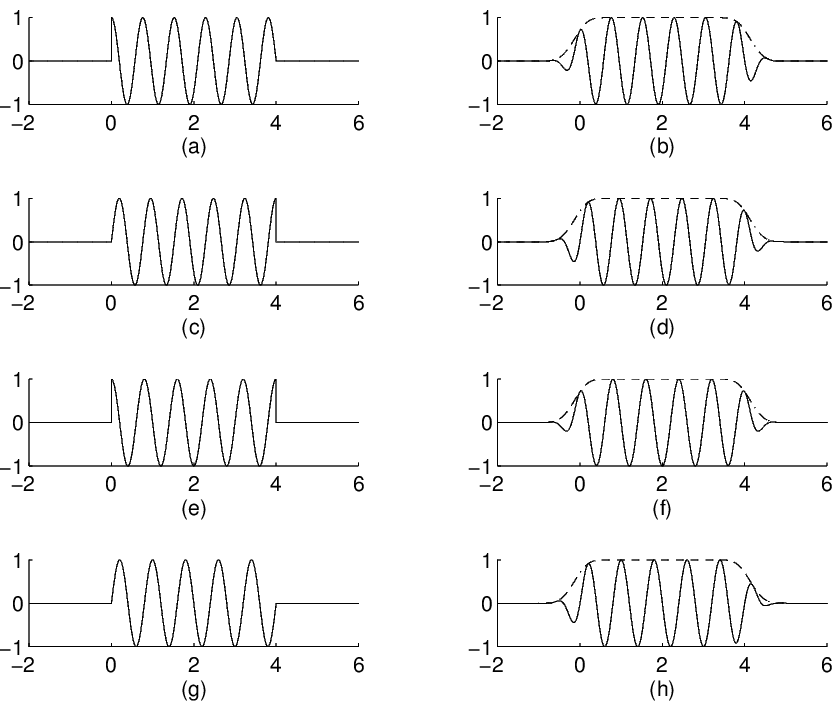
All these bases can be constructed in discrete time by sampling the cosines/sines basis functions [link] . Local cosine bases in discretetime were constructed originally by Malvar and are sometimes called lapped orthogonal transforms [link] . In the discrete case, the efficient implementation of trigonometric transforms(using DCT I-IV and DST I-IV) can be utilized after folding. In this case, expanding in local trigonometric bases corresponds to computinga DCT after preprocesing (or folding) the signal.

For a sample basis function in each of the four bases, [link] shows the corresponding smooth basis function after unfolding. Observe that for local cosine and sine bases,the basis functions are not linear phase; while the window is symmetric, the windowed functions are not. However, for alternating sine/cosinebases the (unfolded) basis functions are linear phase. There is a link between local sine (or cosine) bases and modulated filter banksthat cannot have linear phase filters (discussed in  Chapter: Filter Banks and Transmultiplexers ). So there is also a link between alternating cosine/sine bases and linear-phase modulated filter banks(again see  Chapter: Filter Banks and Transmultiplexers ). This connection is further explored in [link] .

Local trigonometric bases have been applied to several signal processing problems. For example, they have been usedin adaptive spectral analysis and in the segmentation of speech into voiced and unvoiced regions [link] . They are also used for image compression and are knownin the literature as lapped-orthogonal transforms [link] .

Signal adaptive local trigonometric bases

In the adaptive wavelet packet analysis described in [link] , we considered a full filter bank tree of decompositions and used some algorithm(best-basis algorithm, for instance) to prune the tree to get the best tree topology (equivalently frequency partition)for a given signal. The idea here is similar. We partition the time axis (or interval) into bins and successively refine eachpartition into further bins, giving a tree of partitions for the time axis (or interval). If we use smooth local trigonometric basesat each of the leaves of a full or pruned tree, we get a smooth basis for all signals on the time axis (or interval). In adaptivelocal bases one grows a full tree and prunes it based on some criterion to get the optimal set of temporal bins.

[link] schematically shows a sample time-frequency tiling associated with a particular local trigonometric basis.Observe that this is the dual of a wavelet packet tiling (see [link] )—in the sense that one can switch the time and frequency axes to go between the two.