| << Chapter < Page | Chapter >> Page > |
Recall the four orthonormal trigonometric bases for we described earlier.
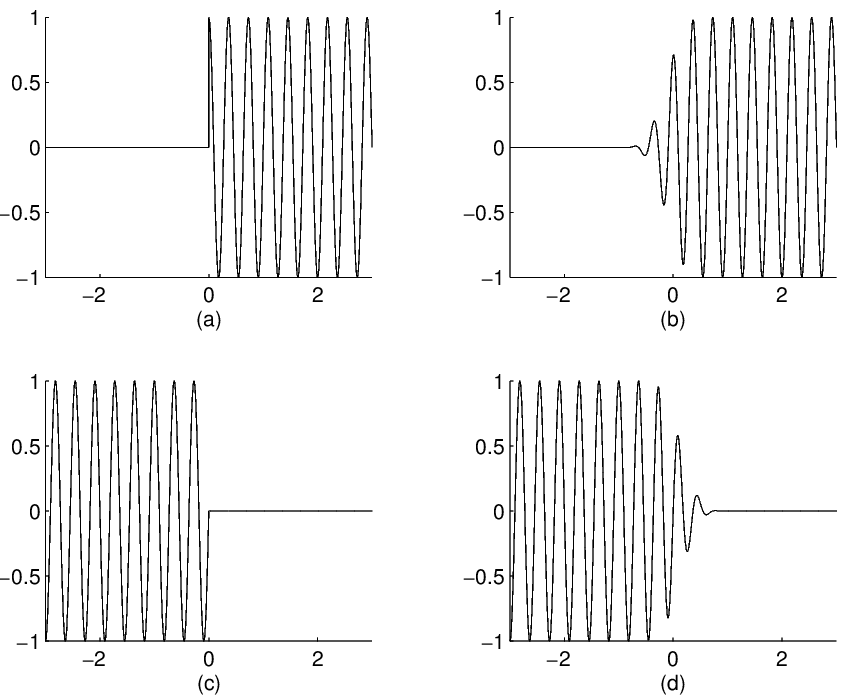
The bases functions have discontinuities at and because they are restrictions of the cosines and sines to the unit interval by rectangular windowing.The natural extensions of these basis functions to (i.e., unwindowed cosines and sines) are either even (say “+”) or odd (say “-”)symmetric (locally) about the endpoints and . Indeed the basis functions for the four cases are , , and symmetric, respectively, at . From the preceding analysis, this means that unfolding these basis functionscorresponds to windowing if the unfolding operator has the right polarity. Also observe that the basis functions are discontinuous atthe endpoints. Moreover, depending on the symmetry at each endpoint all odd derivatives (for “+” symmetry) or evenderivatives (for “ ” symmetry) are zero. By choosing unfolding operators of appropriate polarity at the endpoints (with non overlapping actionregions) for the four bases, we get smooth basis functions of compact support. For example, for (+, ) symmetry, the basis function is supported in and is as many times continuously differentiable as and are.
Let be an ordered set of points in defining a partition into disjoint intervals . Now choose one of the four bases above for each intervalsuch that at the basis functions for and that for have opposite symmetries. We say the polarity at is positive if the symmetry is and negative if it is . At each choose a smooth cutoff function and action radius so that the action intervals do not overlap. Let be the polarity of and define the unitary operator
Let denote all the basis functions for all the intervals put together. Then forms a nonsmooth orthonormal basis for . Simultaneously also forms a smooth
orthonormal basis for . To find the expansion coefficients of a function in this basis we use
In other words, to compute the expansion coefficients of in the new (smooth) basis, one merely folds to and finds its expansion coefficients with respect to the originalbasis. This allows one to exploit fast algorithms available for coefficient computation in the original basis.
So for an arbitrary choice of polarities at the end points we have smooth local trigonometric bases. In particular by choosing the polarityto be positive for all (consistent with the choice of the first basis in all intervals) we get local cosine bases.If the polarity is negative for all (consistent with the choice of the second basis for all intervals), we get localsine bases. Alternating choice of polarity (consistent with the alternating choice of the third and fourth bases in the intervals) thusleads to alternating cosine/sine bases.

Notification Switch
Would you like to follow the 'Wavelets and wavelet transforms' conversation and receive update notifications?