| << Chapter < Page | Chapter >> Page > |
[link] shows that SFFT is easily faster than FFTW on both devices. This contradicts Frigo and Johnson's claim that the performance of FFTW is portable, and tends to support the idea that it is possible to write fast and portable code without exhaustive searches through the configuration space of all possible FFTs.
A considerable amount of effort was needed to work around several problems that were encountered when targeting ARM NEON with Apple clang 3.0, and many of SFFT's primitive macros for NEON were written in inline assembly code. Among the problems encountered when targeting ARM NEON with Apple clang 3.0:
The above problems affect all FFT libraries equally, and it seems that portability depends critically on the quality of the machine specific code and macros.


The accuracy of each FFT was measured as per the methods in Benchmark methods . The accuracy of single and double precision FFTs on an Intel Core i7-2600 is plotted in [link] , and shows that the relative RMS error for FFTW, SFFT and SPIRAL is within an acceptable range. Graphs for all other machines are similar.

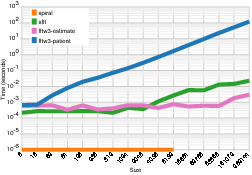
[link] shows that FFTW, in patient mode, requires several orders of magnitude more time to initialize as it searches for a fast FFT configuration. SPIRAL has a very fast setup time, because it is entirely statically elaborated and needs no dynamic initialization. The setup time for SFFT is comparable to FFTW in estimate mode, though SFFT's setup time begins to increase for transforms larger than 8192 points. This is likely because of repeated calls to the complex exponential function as twiddle factor LUTs are elaborated; no effort was made to optimize this setup code, and it is likely that it would be much faster if the calls to the complex exponential function were optimized.
Graphs for all other machines are similar.
Compared to other libraries, SFFT produced larger binaries for the benchmarks, because there is currently no optimization performed between transforms contained in the same library. For 64-bit single precision binaries on OS X with AVX, the size of the SFFT benchmark was approximately 2.8 megabytes while the size of the FFTW benchmark was 1.8 megabytes.
For each size of transform on a particular machine, SFFT chooses the fastest configuration from a set of up to eight possible configurations. Small transforms have only one option, which is a fully hard-coded transform, while larger transforms have up to eight, which could include the four-step transform, and several variants of the hard-coded leaf transform, where each variant corresponds to a particular size of leaf sub-transform and size of body sub-transform, and for size-16 leaf sub-transforms, a streaming store variant is included too. The decision of exactly which configuration to use depends on the size of transform, the compiler, and the characteristics of the host machine.

Notification Switch
Would you like to follow the 'Computing the fast fourier transform on simd microprocessors' conversation and receive update notifications?