| << Chapter < Page | Chapter >> Page > |
Entering known values in this equation yields,
The value of is now entered into the expression for , which yields
Strategy for (b)
The kinetic energy before the collision is the incoming disk’s translational kinetic energy, and after the collision, it is the rotational kinetic energy of the two stuck together.
Solution for (b)
First, we calculate the translational kinetic energy by entering given values for the mass and speed of the incoming disk.
After the collision, the rotational kinetic energy can be found because we now know the final angular velocity and the final moment of inertia. Thus, entering the values into the rotational kinetic energy equation gives
Strategy for (c)
The linear momentum before the collision is that of the disk. After the collision, it is the sum of the disk’s momentum and that of the center of mass of the stick.
Solution of (c)
Before the collision, then, linear momentum is
After the collision, the disk and the stick’s center of mass move in the same direction. The total linear momentum is that of the disk moving at a new velocity plus that of the stick’s center of mass,
which moves at half this speed because . Thus,
Gathering similar terms in the equation yields,
so that
Substituting known values into the equation,
Discussion
First note that the kinetic energy is less after the collision, as predicted, because the collision is inelastic. More surprising is that the momentum after the collision is actually greater than before the collision. This result can be understood if you consider how the nail affects the stick and vice versa. Apparently, the stick pushes backward on the nail when first struck by the disk. The nail’s reaction (consistent with Newton’s third law) is to push forward on the stick, imparting momentum to it in the same direction in which the disk was initially moving, thereby increasing the momentum of the system.
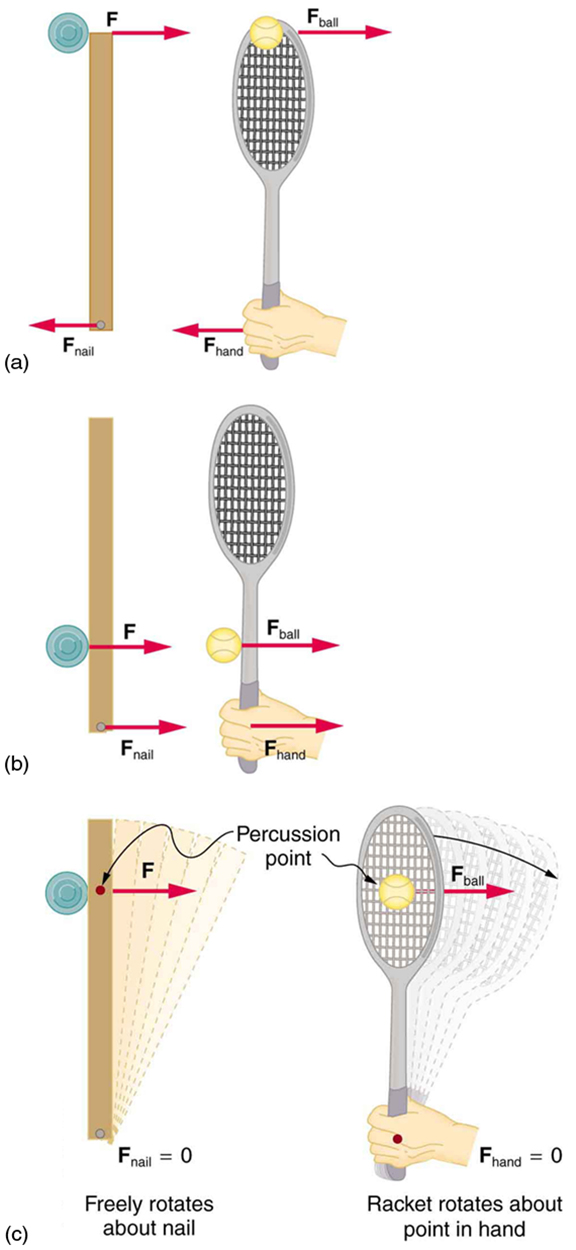
The above example has other implications. For example, what would happen if the disk hit very close to the nail? Obviously, a force would be exerted on the nail in the forward direction. So, when the stick is struck at the end farthest from the nail, a backward force is exerted on the nail, and when it is hit at the end nearest the nail, a forward force is exerted on the nail. Thus, striking it at a certain point in between produces no force on the nail. This intermediate point is known as the percussion point .
An analogous situation occurs in tennis as seen in [link] . If you hit a ball with the end of your racquet, the handle is pulled away from your hand. If you hit a ball much farther down, for example, on the shaft of the racquet, the handle is pushed into your palm. And if you hit the ball at the racquet’s percussion point (what some people call the “sweet spot”), then little or no force is exerted on your hand, and there is less vibration, reducing chances of a tennis elbow. The same effect occurs for a baseball bat.
Is rotational kinetic energy a vector? Justify your answer.
No, energy is always scalar whether motion is involved or not. No form of energy has a direction in space and you can see that rotational kinetic energy does not depend on the direction of motion just as linear kinetic energy is independent of the direction of motion.
Twin skaters approach one another as shown in [link] and lock hands. (a) Calculate their final angular velocity, given each had an initial speed of 2.50 m/s relative to the ice. Each has a mass of 70.0 kg, and each has a center of mass located 0.800 m from their locked hands. You may approximate their moments of inertia to be that of point masses at this radius. (b) Compare the initial kinetic energy and final kinetic energy.
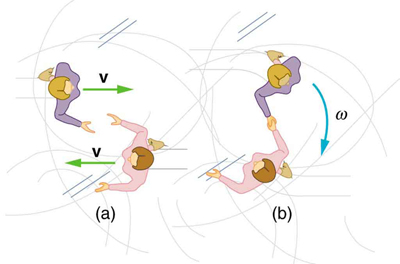
(a) 3.13 rad/s
(b) Initial KE = 438 J, final KE = 438 J
Suppose a 0.250-kg ball is thrown at 15.0 m/s to a motionless person standing on ice who catches it with an outstretched arm as shown in [link] .
(a) Calculate the final linear velocity of the person, given his mass is 70.0 kg.
(b) What is his angular velocity if each arm is 5.00 kg? You may treat the ball as a point mass and treat the person's arms as uniform rods (each has a length of 0.900 m) and the rest of his body as a uniform cylinder of radius 0.180 m. Neglect the effect of the ball on his center of mass so that his center of mass remains in his geometrical center.
(c) Compare the initial and final total kinetic energies.


Notification Switch
Would you like to follow the 'Unit 8 - rotational motion' conversation and receive update notifications?