0.5 Sampling with automatic gain control  (Page 18/19)

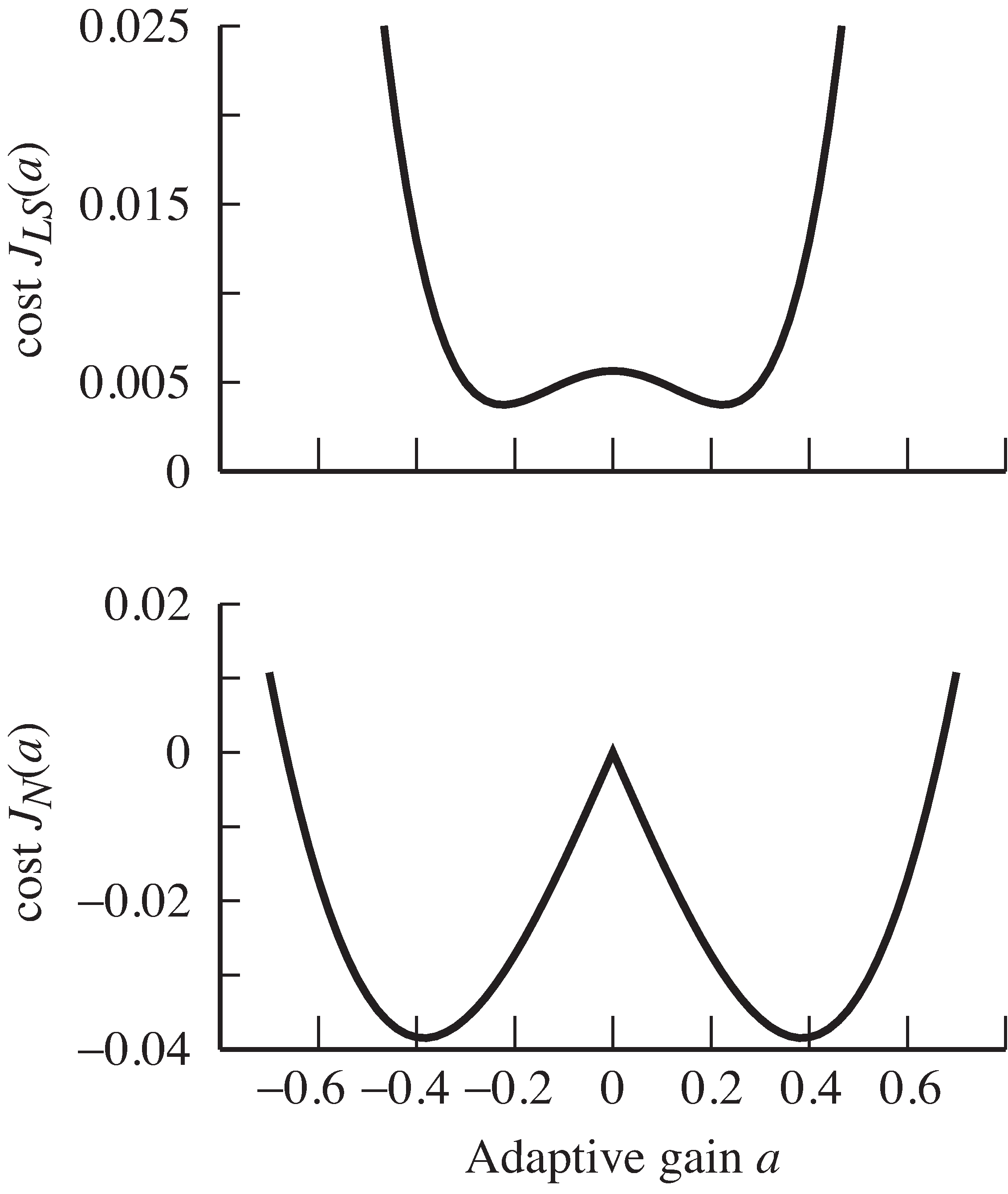
But why do the two algorithms converge to different places? The facile answer is that they are different becausethey minimize different performance functions. Indeed, the error surfaces in [link] show minima in different locations. The convergent value of $a\approx 0.38$ for $J_N\left(a\right)$ is explicable because $0.{38}^2\approx 0.15={\mathbf{s}}^2$ . The convergent value of $a=0.22$ for $J_{LS}\left(a\right)$ is calculated in closed form in Exercise  [link] , and this value does a good job minimizing its cost,but it has not solved the problem of making $a^2$ close to ${\mathbf{s}}^2$ . Rather, $J_{LS}\left(a\right)$ calculates a smaller gain that makes $\text{avg}\left\{s^2\right\}\approx {\mathbf{s}}^2$ . The minima are different. The moral is this:Be wary of your performance functions—they may do what you ask.

Using an agc to combat fading

One of the impairments encountered in transmission systems is the degradation due to fading, when the strengthof the received signal changes in response to changes in the transmission path. (Recall the discussion in [link] .) This section shows how an AGC can be used to counteractthe fading, assuming the rate of the fading is slow, and provided the signal does not disappear completely.

Suppose that the input consists of a random sequence undulating slowly up and down in magnitude, as in the topplot of [link] . The adaptive AGC compensates for the amplitude variations,growing small when the power of the input is large, and large when the power of the input is small. This is shown in themiddle graph. The resulting output is of roughly constant amplitude, as shown in the bottom plot of [link] .