| << Chapter < Page | Chapter >> Page > |
There are two basic approaches to an AGC. The traditional approach uses analog circuitry to adjust the gain before the sampling. The more modern approach uses the output of the sampler to adjust thegain. The advantage of the analog method is that the two blocks (the gain and the sampling) are separate and do not interact.The advantage of the digital adjustment is that less additional hardware is required since the DSP processing is already presentfor other tasks.
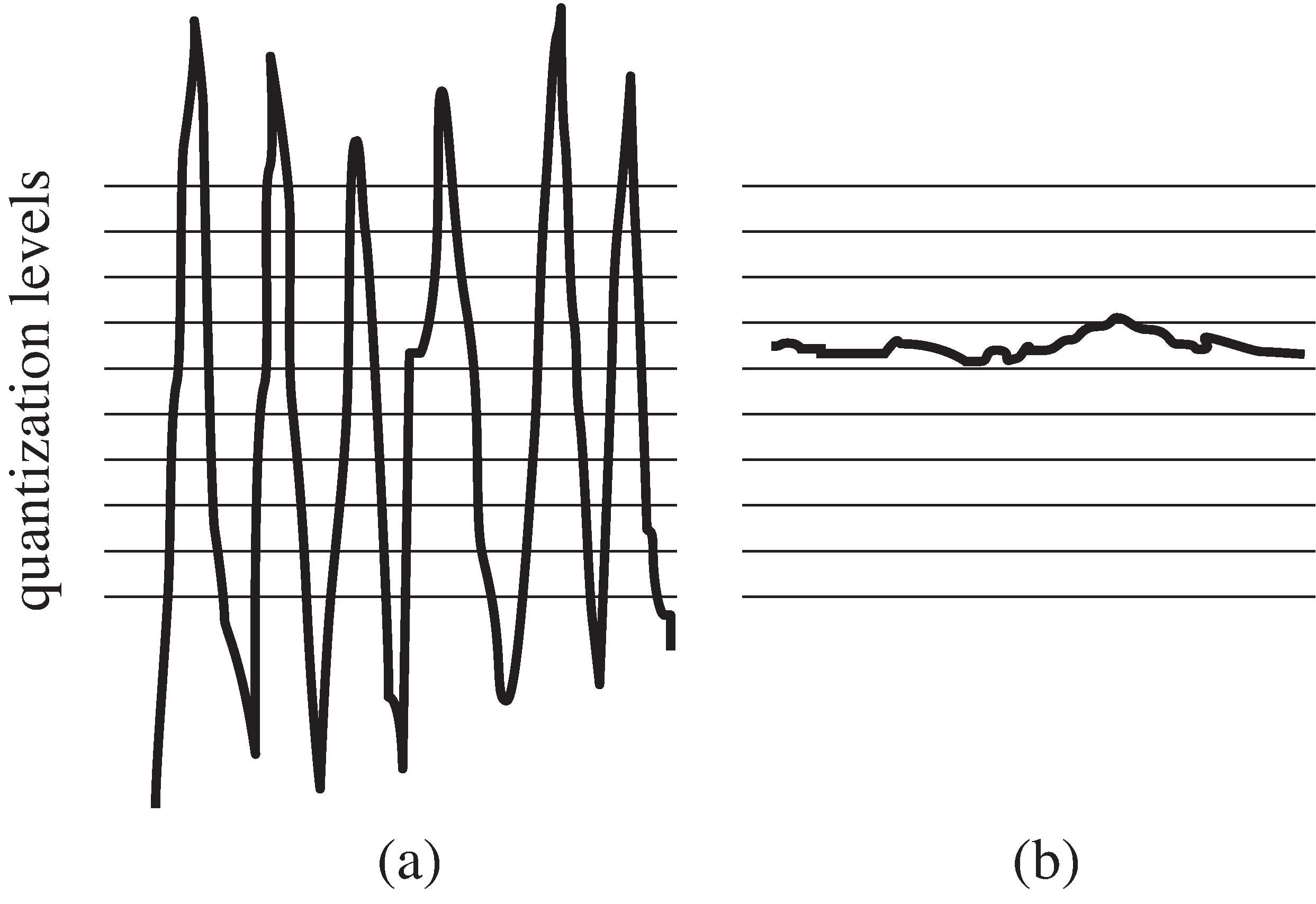
A simple digital system for AGC gain adjustment is shown in [link] . The input is multiplied by the gain to give the normalized signal . This is then sampled to give the output . The assessment block measures and determines whether must be increased or decreased.
The goal is to choose so that the power (or average energy) of is approximately equal to some specified . Since
it would be ideal to choose
because this would imply that . The averaging operation (in this case a movingaverage over a block of data of size ) is defined by
Unfortunately, neither the analog input nor its power are directly available to the assessment blockin the DSP portion of the receiver, so it is not possible to directly implement [link] .
Is there an adaptive element that can accomplish this task? As suggested in the beginning of "Iteration and Optimization" , there are three steps to the creation of a viableoptimization approach: setting a goal, choosing a solution method, and testing. As in any real life engineering task, a propermathematical statement of the goal can be tricky, and this section proposes two (slightly different) possibilitiesfor the AGC. By comparing the resulting algorithms (essentially, alternativeforms for the AGC design), it may be possible to trade off among various design considerations.
One sensible goal is to try to minimize a simple function of the difference between the power of the sampled signal and the desired power . For instance, the averaged squared error in the powers of and ,
penalizes values of which cause to deviate from . This formally mimics the parabolic form of the objective [link] in the polynomial minimization example of the previous section.Applying the steepest descent strategy yields
which is the same as [link] , except that the name of the parameter has changed from to . To find the exact form of [link] requires the derivative of with respect to the unknown parameter . This can be approximated by swapping the derivative and the averaging operations to give

Notification Switch
Would you like to follow the 'Software receiver design' conversation and receive update notifications?