| << Chapter < Page | Chapter >> Page > |
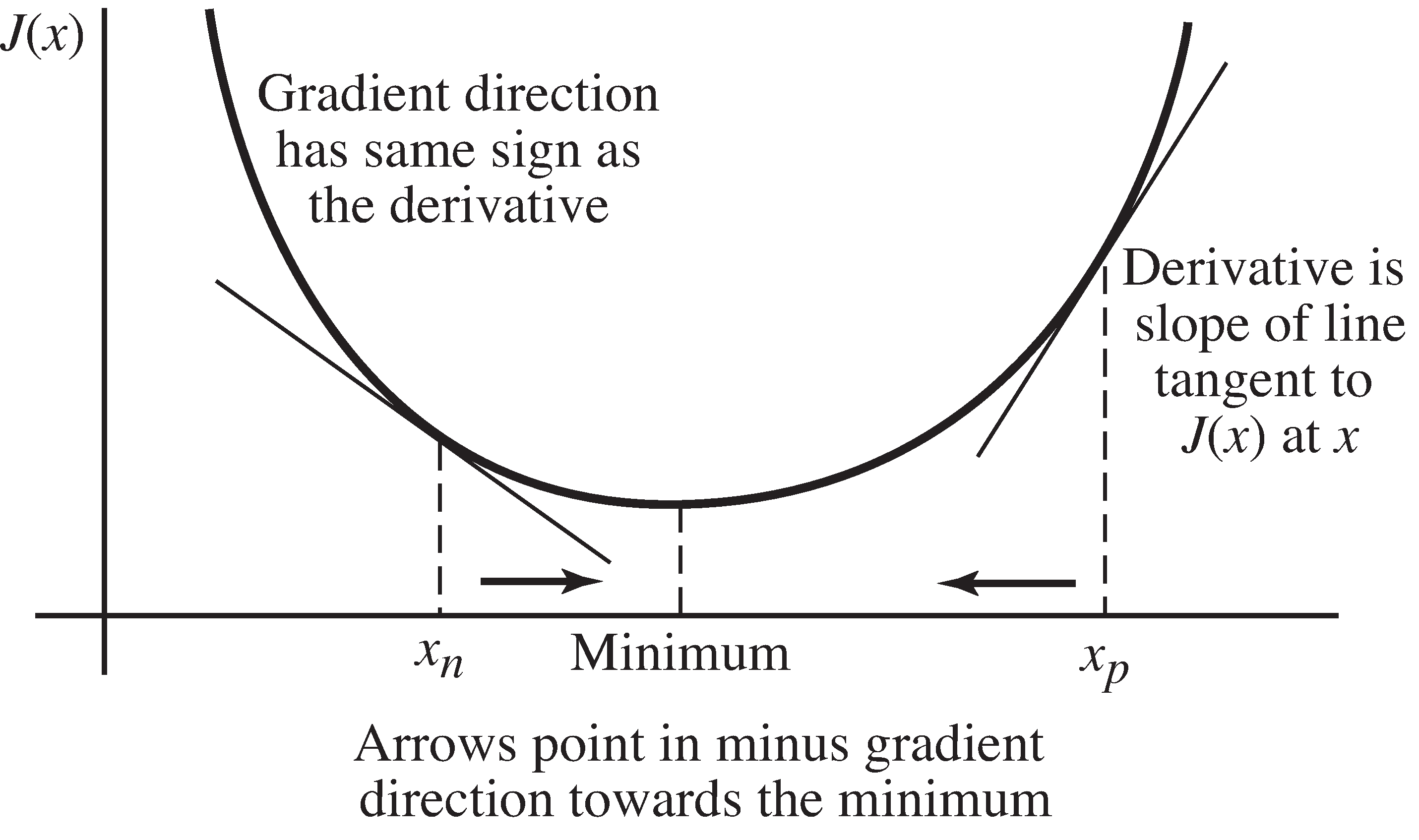
To apply steepest descent to the minimization of the polynomial in [link] , suppose that a current estimate of is available at time , which is denoted . A new estimate of at time can be made using
where is a small positive number called the stepsize, and where the gradient (derivative) of is evaluated at the current point . This is then repeated again and again as increments. This procedure isshown in [link] . When the current estimate is to the right of the minimum, the negative of the gradient points left. When the current estimate is to the left of the minimum, thenegative gradient points to the right. In either case, as long as the stepsize is suitably small, the newestimate is closer to the minimum than the old estimate ; that is, is less than .
To make this explicit, the iteration defined by [link] is
or, rearranging,
In principle, if [link] is iterated over and over, the sequence should approach the minimum value . Does this actually happen?
There are two ways to answer this question. It is
straightforward to simulate the process. Here is some M
atlab code
that takes an initial estimate of
called
x(1) and iterates
[link] for
N=500 steps.
N=500; % number of iterations
mu=.01; % algorithm stepsizex=zeros(1,N); % initialize x to zero
x(1)=3; % starting point x(1)for k=1:N-1
x(k+1)=(1-2*mu)*x(k)+4*mu; % update equationend
polyconverge.m find the minimum of
via steepest descent
(download file)
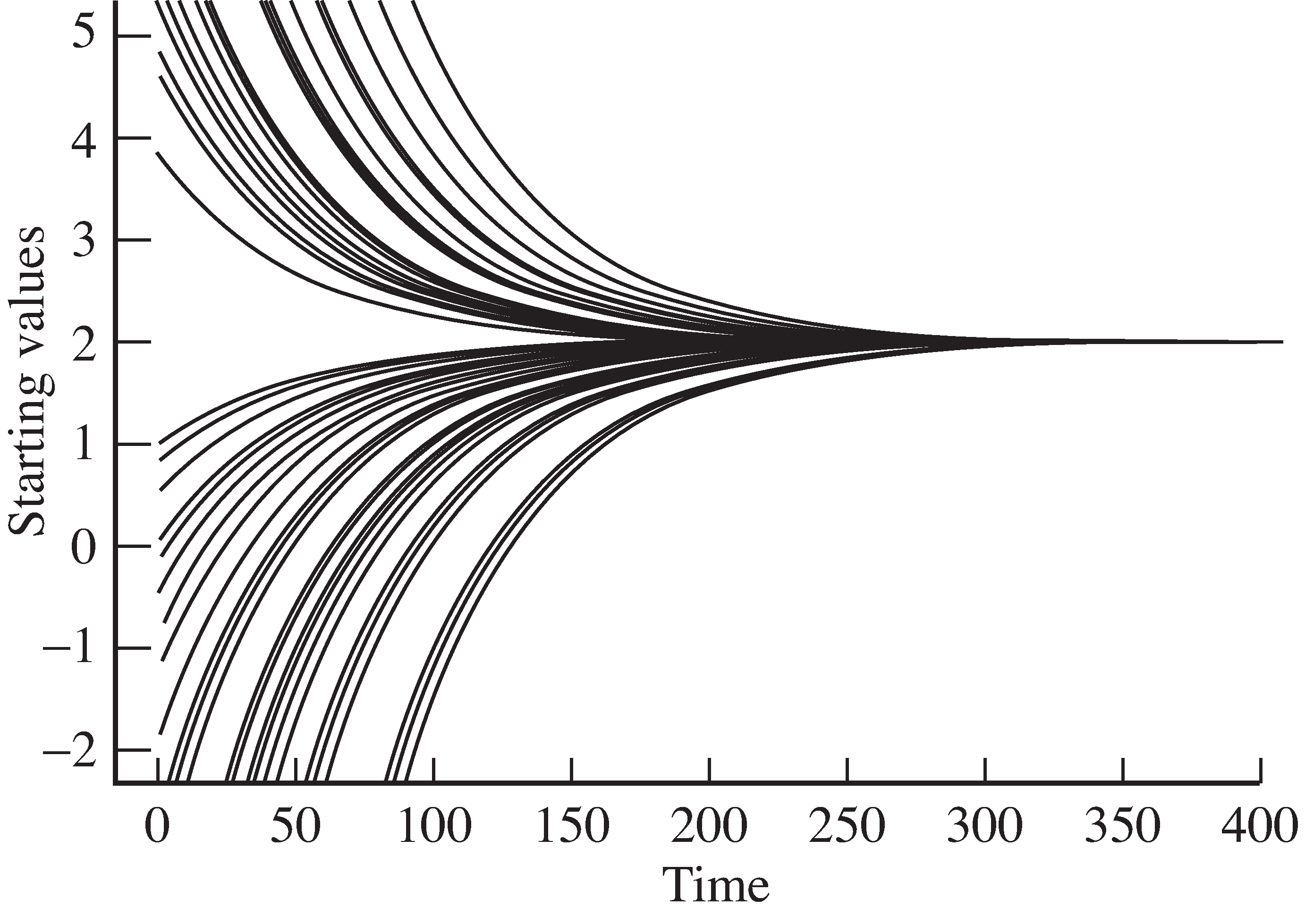
[link] shows the output of
polyconverge.m for 50 different
x(1) starting values superimposed;
all converge smoothly to the minimum at
.
Explore the behavior of steepest descent by running
polyconverge.m with different parameters.
mu = -.01, 0, .0001, .02, .03, .05, 1.0, 10.0.
Can
mu be too large or too small?N= 5, 40, 100, 5000. Can
N be too
large or too small?x(1) .
Can
x(1) be too
large or too small?As an alternative to simulation, observe that the process [link] is itself a linear time invariant system, of the general form
which is stable as long as . For a constant input, the final value theorem of z-Transforms (see [link] ) can be used to show that the asymptotic (convergent)output value is . To see this withoutreference to arcane theory, observe that if is to converge, then it must converge to some value, say . At convergence, , and so [link] implies that , which implies that . (This holds assuming .) For example, for [link] , , which is indeed the minimum.
Thus, both simulation and analysis suggest that the iteration [link] is a viable way to find the minimum of the function , as long as is suitably small. As will become clearer in later sections, suchsolutions to optimization problems are almost always possible—as long as the function is differentiable. Similarly, it is usually quite straightforward to simulate thealgorithm to examine its behavior in specific cases, though it is not always so easy to carry out a theoretical analysis.

Notification Switch
Would you like to follow the 'Software receiver design' conversation and receive update notifications?