| << Chapter < Page | Chapter >> Page > |
where is the amplitude, the wavelength and is a phase shift . The phase shift accounts for the fact that the wave at does not start at the equilibrium position. A function of time would be:
where is the period of the wave. Descriptions of the wave incorporate the amplitude, wavelength, frequency or period and a phase shift.

We have seen that when a pulse meets a fixed endpoint, the pulse is reflected, but it is inverted. Since a transverse wave is a series of pulses, a transverse wave meeting a fixed endpoint is also reflected and the reflected wave is inverted. That means that the peaks and troughs are swapped around.

If transverse waves are reflected from an end, which is free to move, the waves sent down the string are reflected but do not suffer a phase shift as shown in [link] .

What happens when a reflected transverse wave meets an incident transverse wave? When two waves move in opposite directions, through each other, interference takes place. If the two waves have the same frequency and wavelength then standing waves are generated.
Standing waves are so-called because they appear to be standing still.
Tie a rope to a fixed object such that the tied end does not move. Continuously move the free end up and down to generate firstly transverse waves and later standing waves.
We can now look closely how standing waves are formed. [link] shows a reflected wave meeting an incident wave.

When they touch, both waves have an amplitude of zero:

If we wait for a short time the ends of the two waves move past each other and the waves overlap. To find the resultant wave, we add the two together.

In this picture, we show the two waves as dotted lines and the sum of the two in the overlap regionis shown as a solid line:
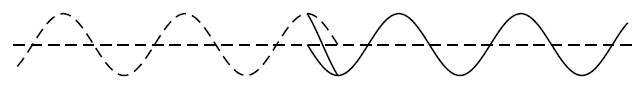
The important thing to note in this case is that there are some points where the two waves always destructively interfere to zero.If we let the two waves move a little further we get the picture below:

Again we have to add the two waves together in the overlap region to see what the sum of the waves looks like.
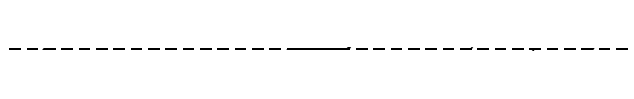
In this case the two waves have moved half a cycle past each other but because they are completely out of phase they cancel out completely.
When the waves have moved past each other so that they are overlapping for a large region the situation looks like a waveoscillating in place. The following sequence of diagrams show what the resulting wave will look like. To make it clearer, the arrows atthe top of the picture show peaks where maximum positive constructive interference is taking place. The arrows at the bottomof the picture show places where maximum negative interference is taking place.

Notification Switch
Would you like to follow the 'Physics - grade 10 [caps 2011]' conversation and receive update notifications?