| << Chapter < Page | Chapter >> Page > |
Now for the fun. Because , each of the half-length transforms can be reduced to two quarter-length transforms, each of these to twoeighth-length ones, etc. This decomposition continues until we are left with length-2 transforms. This transform is quitesimple, involving only additions. Thus, the first stage of the FFT has length-2 transforms (see the bottom part of [link] ). Pairs of these transforms are combined by adding one to the other multiplied by a complexexponential. Each pair requires 4 additions and 2 multiplications, giving a total number of computations equaling . This number of computations does not change from stage to stage.Because the number of stages, the number of times the length can be divided by two, equals , the number of arithmetic operations equals , which makes the complexity of the FFT .
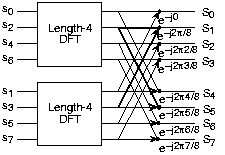

Doing an example will make
computational savings more obvious. Let's look at the detailsof a length-8 DFT. As shown on
[link] , we first decompose the DFT into two length-4
DFTs, with the outputs added and subtracted together in pairs.Considering
[link] as the
frequency index goes from 0 through 7, we recycle values fromthe length-4 DFTs into the final calculation because of the
periodicity of the DFT output. Examining how pairs of outputsare collected together, we create the basic computational
element known as a
butterfly (
[link] ).
Butterfly

Note that the ordering of the input sequence in the two parts of [link] aren't quite the same. Why not? How is the ordering determined?
The upper panel has not used the FFT algorithm to compute the length-4 DFTs while the lower one has. The ordering isdetermined by the algorithm.
Other "fast" algorithms were discovered, all of which make use of how many common factors the transformlength has. In number theory, the number of prime factors a given integer has measures how composite it is. The numbers 16 and 81 are highly composite (equaling and respectively), the number 18 is less so ( ), and 17 not at all (it's prime). In over thirty years of Fourier transform algorithm development, the originalCooley-Tukey algorithm is far and away the most frequently used. It is so computationally efficient that power-of-twotransform lengths are frequently used regardless of what the actual length of the data.
Suppose the length of the signal were ? How would you compute the spectrum of this signal using the Cooley-Tukeyalgorithm? What would the length of the transform be?
The transform can have any greater than or equal to the actual duration of the signal. We simply“pad” the signal with zero-valued samples until a computationally advantageous signal length results. Recallthat the FFT is an algorithm to compute the DFT . Extending the length of the signal this way merely means weare sampling the frequency axis more finely than required. To use the Cooley-Tukey algorithm, the length of theresulting zero-padded signal can be 512, 1024, etc. samples long.

Notification Switch
Would you like to follow the 'Discrete-time fourier analysis' conversation and receive update notifications?