| << Chapter < Page | Chapter >> Page > |
Suppose that we first choose the simple case with uniform weighting, that is, for and, therefore, . In this case, is given by
The magnitude of this transfer function is plotted in [link] . From this plot we can conclude that the pulse response has what might be generally considered to be the frequency response of a bandpass filter. The filter is centered on bin m and its bandwidth is nominally . While it might be characterized as a bandpass filter, we also note that the passband is quite rounded and the stopband rejection is relatively poor. The first sidelobes are only 13 dB lower than the peak of the passband response.
We've now shown that the path from the input to the m-th bin can be described as a finite impulse response (FIR) filtering operation and that the transfer function of that filtering operation has a fairly sloppy bandpass characteristic, at least when the data weighting is uniform. What happens for other values of m then? The answer is "the same thing." For each value of m between 0 and , the pulse response is computed, leading to the transfer function . An overlay of these bandpass responses is shown in the lower portion of [link] . From this we can conclude that the block diagram shown in [link] describes a single-input, N-output bank of filters. The filter center frequencies are spaced uniformly in increments of Hz. All N outputs are sampled in time as frequently as the input. When the weighting function is uniform, then the bandpass filters have the form of [link] , shown in [link] .
![Figure seven contains two parts. Part a is labeled Transfer Function H_m(f) of processing from input x(k) to the DFT Output Bin X_m(k). It is the first quadrant of a cartesian graph, with vertical axis labeled Transfer Function H_m(f), and horizontal axis labeled Frequency (Hz). The horizontal axis contains the following labeled points from left to right: -f_s/2, 0, [(m-1)f_s]/N mf_s/N, [(m+1)f_s]/N + f_s/2. The graph contains seven rounded peaks that return to points on the horizontal axis. The peaks are uneven and deformed in shape. The second label corresponds with the fourth point, the third label corresponds with the fifth point, the fourth label corresponds with the sixth peak, and the fifth label corresponds with the sixth point. The sixth peak is significantly larger than any of the other peaks on the graph. Part b is labeled Overlay of Transfer Function for all N DFT Bin Outputs X_m(f), 0 ≤ m ≤ N-1. The vertical axis is labeled Transfer Function H;(f), and the horizontal axis is labeled Frequency (Hz). The graph consists of a series of uniform crossing peaked curves. A new curve begins from the origin at each point that the previous curve reaches its apex, meaning at each marked point on the graph there is a curve at its apex, a curve ending at the horizontal axis, and a curve just beginning on the horizontal axis. These points are labeled -f_s/2, m-1, m, m+1, 0, n-1, n, n+1 ⋅⋅ f_s/2.](/ocw/mirror/col11165_1.2_complete/m32670/fig11.png)
We've just shown that the DFT of delayed versions of the input sequence has the general properties of a bank of regularly-spaced bandpass filters. Two considerations leave us short of our goals. The first is that the shape of the transfer function for each bandpass filter is not good enough for most applications and must be improved. The second is that of reducing the amount of computation required. We address the first one in this section, and temporarily defer the computation issue.
[link] shows two transfer functions. The one pointed to from the left is exactly the same as that shown in [link] and defined in [link] . The one pointed to from the right is representative of the type needed for demultiplexing FDM multichannel telephone signals. It offers essentially flat response for most of the passband, has very sharp transition bands, and suppresses all energy outside of the transition bands by 55 dB or more. While other applications may require different transfer functions, as a rule they will be much more stringent than unweighted transfer function shown in [link] .
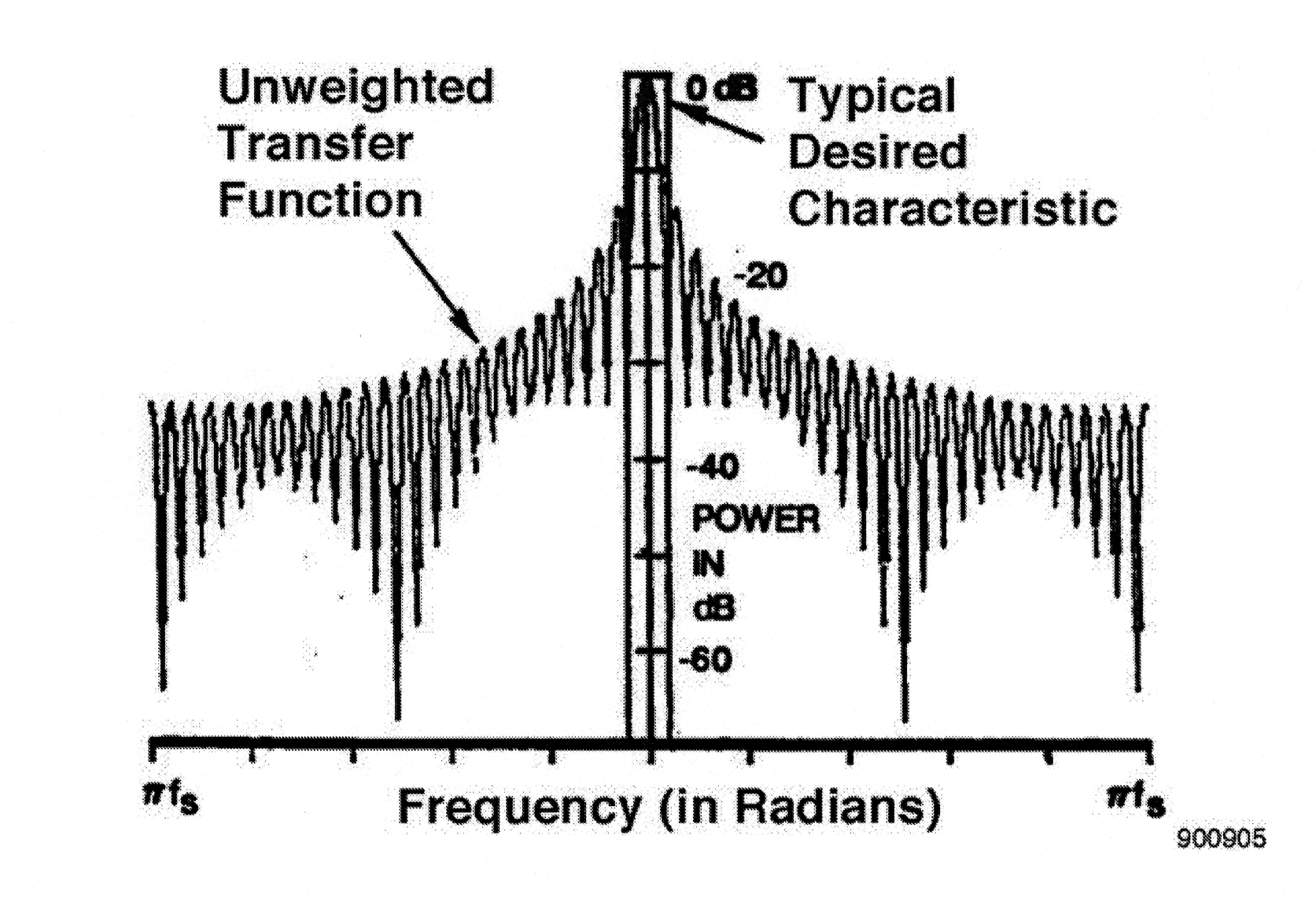
How then do we attain different transfer function characteristics? In fact, we use some of the remaining degrees of freedom, the weighting function . By allowing to be non-uniform we can now alter the shape of the transfer function of each bandpass filter. By using well-known FIR filter design techniques (see An Introduction to the FDM-TDM Digital Transmultiplexer: Appendix A ) it is possible to attain virtually any shape. It is not, however, possible to always attain the desired shape and the desired bandwidth while keeping the duration of the pulse response constant. In fact, as discussed in An Introduction to the FDM-TDM Digital Transmultiplexer: Appendix A , for a constant bandwidth, the pulse response duration must grow as the transition bandwidth is forced to be smaller and as the stopband suppression in increased. The chain of events described in [link] then unfolds.

Notification Switch
Would you like to follow the 'An introduction to the fdm-tdm digital transmultiplexer' conversation and receive update notifications?