0.18 Game theory  (Page 2/4)

We find the saddle point by placing an asterisk next to the minimum entry in each row, and by putting a box around the maximum entry in each column as shown below.

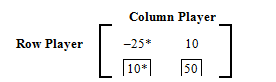
Since the second row, first column entry, which happens to be 10, has both an asterisk and a box, it is a saddle point. This implies that the value of the game is 10, and the optimal strategy for the row player is to always play row 2, and the optimal strategy for the column player is to always play column 1. If both players play their optimal strategies, the row player will win 10 units each time.

The row player's strategy is written as $\left[\begin{array}{cc}0& 1\end{array}\right]$ indicating that he will play row 1 with a probability of 0 and row 2 with a probability of 1. Similarly the column player's strategy is written as $\left[\begin{array}{c}1\\ 0\end{array}\right]$ implying that he will play column 1 with a probability of 1, and column 2 with a probability of 0.

We write the payoff matrix for Robert as follows:

To determine whether the game is strictly determined, we look for a saddle point. Again, we place an asterisk next to the minimum value in each row, and a box around the maximum value in each column. We get

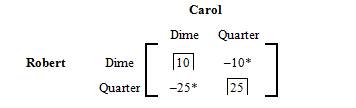
Since there is no entry that has both an asterisk and a box, the game does not have a saddle point, and thus it is non-strictly determined.

We wish to devise a strategy for Robert. If Robert consistently shows a dime, for example, Carol will see the pattern and will start showing a quarter, and Robert will lose. Conversely, if Carol repeatedly shows a quarter, Robert will start showing a quarter, thus resulting in Carol's loss. So a good strategy is to throw your opponent off by showing a dime some of the times and showing a quarter other times. Before we develop an optimal strategy for each player, we will consider an arbitrary strategy for each and determine the corresponding payoffs.