| << Chapter < Page | Chapter >> Page > |
In this chapter, you will learn to:
Game theory is one of the newest branches of mathematics. It first came to light when a brilliant mathematician named Dr. John von Neumann co-authored with Dr. Morgenstern a book titled Theory of Games and Economic Behavior . Since then it has played an important role in decision making in business, economics, social sciences and other fields.
In this chapter, we will study games that involve only two players. In these games, since a win for one person is a loss for the other, we refer to them as two-person zero-sum games . Although the games we will study here are fairly simple, they will provide us with an understanding of how games work and how they are applied in practical situations. We begin with an example.
Robert and Carol decide to play a game using a dime and a quarter. Each chooses one of the two coins, puts it in their hand and closes their fist. At a given signal, they simultaneously open their fists. If the sum of the coins is less than thirty five cents, Robert gets both coins, otherwise, Carol gets both coins. Write the matrix for the game, determine the optimal strategies for each player, and find the expected payoff for Robert.
Suppose Robert is the row player, that is, he plays the rows, and Carol is a column player. If Robert shows a dime and Carol shows a dime, the sum will be less than thirty five cents and Robert will win ten cents. But, if Robert shows a dime and Carol shows a quarter, the sum will not be less than thirty five cents and Carol will win ten cents or Robert will lose ten cents. The following matrix depicts all four cases and their corresponding payoffs for Robert. Remember a negative value is a loss for Robert and a win for Carol.
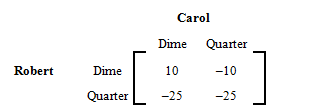
The best strategy for Robert is to always show a dime because this way the worst he can do is lose ten cents. And, the best strategy for Carol is to always show a quarter because that way the worst she can do is to lose ten cents. If both Robert and Carol play their optimal strategies, Robert will lose ten cents each time. Therefore, the value of the game is negative ten cents.
In [link] , since there is only one fixed optimal strategy for each player, regardless of their opponent's strategy, we say the game possesses a pure strategy and is strictly determined .
Next, we formulate a method to find the optimal strategy for each player and the value of the game. The method involves considering the worst scenario for each player.
To consider the worst situation, the row player considers the minimum value in each row, and the column player considers the maximum value in each column. Note that the maximum value really represents a minimum value for the column player because the game matrix depicts the payoffs for the row player. We list the method below.

Notification Switch
Would you like to follow the 'Applied finite mathematics' conversation and receive update notifications?