| << Chapter < Page | Chapter >> Page > |
Mark four points with pins
Assume that the lower left corner of the square is the origin with coordinates of x=0 and y=0. Place pins at the following coordinate positions:
Draw vectors
Now use rubber bands or pipe cleaners to draw the following force vectors originating at the locations of the pins. (Positive angles are measured counter-clockwise relative to the positive xaxis.)
Tactile graphics
The svg file that is required to create tactile graphics for this exercise is named Phy1110a1.svg. You should have downloaded that file earlier. This file contains a vector diagram that represents the instructions given above .
Figure 1 shows the mirror image that is contained in that file for the benefit of your assistant who will create the tactile graphicfor this exercise.
| Figure 1 . Mirror image from the file named Phy1110a1.svg. |
|---|
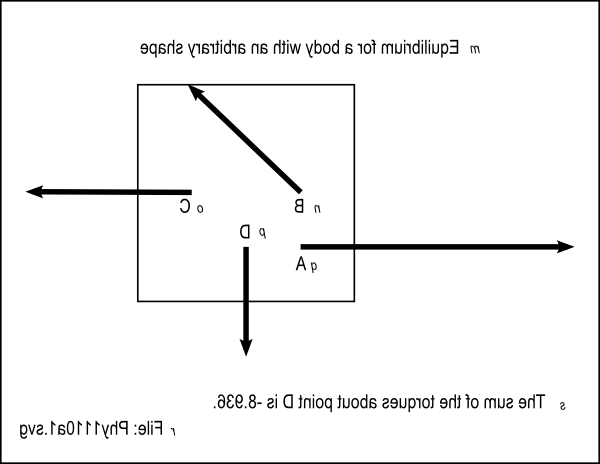 |
Figure 2 shows a non-mirror-image version of the same image.
| Figure 2 . Non-mirror-image version of the image from the file named Phy1110a1.svg. |
|---|
 |
Figure 3 shows the key-value pairs that go with the image in the file named Phy1110a1.svg.
| Figure 3 . Key-value pairs for the image in the file named Phy1110a1.svg. |
|---|
m: Equilibrium for a body with an arbitrary shape
n: Bo: C
p: Dq: A
r: File: Phy1110a1.svgs: The sum of the torques about point D is - 8.936. |
Compute the vector sum of the forces
Begin by computing the horizontal and vertical components of the force at B. As you know by now, the horizontal component is equal to the magnitude ofthe vector (2.8) multiplied by the cosine of 45 degrees and the vertical component is equal to the magnitude of the vector multiplied by the sine of 45degrees. Both the sine and the cosine of 45 degrees is 0.707, so the horizontal and vertical components are both equal to 2. (Obviously, I planned it that way.)
The horizontal and vertical components
The remaining vectors are either horizontal or vertical so no trigonometry is required to compute their components.
The horizontal components of all the vectors consist of:
The sum of the horizontal components is 0.
The vertical components of all the vectors consist of:
The sum of the vertical components is also 0. Therefore, the system exhibits the first condition of equilibrium.
Compute the moment or torque
The second condition for equilibrium states that the sum of all torques acting on the body measured about any axis must be zero.
You can often reduce the complexity of the computation for computing torque by judicious selection of the point about which the torque will be computed.
Compute the torque about point D
In this case, we can simplify the arithmetic by choosing an axis that goes through the point at D.
If you examine your graph, you will see that the line of action for forces A and D both go through the point at D. Therefore, neither of those forces createsa moment about point D so we can exclude them from our computation.

Notification Switch
Would you like to follow the 'Accessible physics concepts for blind students' conversation and receive update notifications?