| << Chapter < Page | Chapter >> Page > |
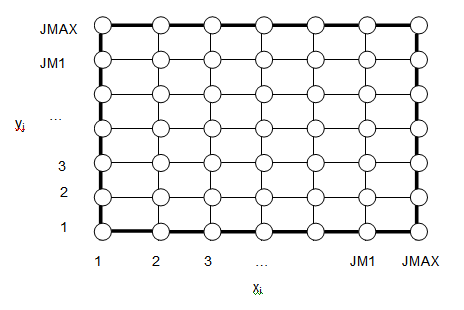
The unit square is now discretized into JMAX by JMAX grid points where the boundary conditions and dependent variables will be evaluated. The grid spacing is . The first and last row and column are boundary values.
The partial derivatives will be approximated by finite differences. For example, the second derivative of vorticity is discretized by a Taylor's series.
The finite difference approximation to the PDE at the interior points results in the following set of equations.
The vorticity at the boundary is discretized and expressed in terms of the components of velocity at the boundary, the stream function values on the boundary and a stream function value in the interior grid. (A greater accuracy is possible by using two interior points.) The stream function at the first interior point from the boundary is written with a Taylor's series as follows.
The choice of sign depends on whether is increasing or decreasing at the boundary. Similarly, on a boundary,
The boundary condition on the stream function is specified by the normal component of velocity at the boundaries. Since we have assumed zero normal component of velocity, the stream function is a constant on the boundary, which we specify to be zero.
The stream function at the boundary is calculated from the normal component of velocity by numerical integration using the trapezodial rule, e.g.,
The finite difference equations for the PDE and the boundary conditions are a linear system of equations with two dependent variables. The dependent variables at a , grid point will be represented as a two component vector of dependent variables,
The pair of equations for each grid point can be represented in the following form
Each coefficient is a 2x2 matrix. For example,
The components of the 2x2 coefficient matrix are the coefficients from the difference equations. The first row is coefficients for the stream function equation and the second row is coefficients for the vorticity equation. The first column is coefficients for the stream function variable and the second column is the coefficients for the vorticity variable. For example, at interior points not affected by the boundary conditions,
The coefficients for the interior grid points adjacent to a boundary are modified as a result of substitution the boundary value of stream function or the linear equation for the boundary vorticity into the difference equations. The stream function equation is coupled to the vorticity with the coefficient and the vorticity equation is coupled to the stream function through the boundary conditions. For example, at a boundary, the coefficients will be modified as follows.

Notification Switch
Would you like to follow the 'Transport phenomena' conversation and receive update notifications?