| << Chapter < Page | Chapter >> Page > |
To better understand the normative approach, imagine two new mothers, Louisa and Kimberly, who are close friends and have children around the same age. Louisa’s daughter is 14 months old, and Kimberly’s son is 12 months old. According to the normative approach, the average age a child starts to walk is 12 months. However, at 14 months Louisa’s daughter still isn’t walking. She tells Kimberly she is worried that something might be wrong with her baby. Kimberly is surprised because her son started walking when he was only 10 months old. Should Louisa be worried? Should she be concerned if her daughter is not walking by 15 months or 18 months?
There are many different theoretical approaches regarding human development. As we evaluate them in this chapter, recall that developmental psychology focuses on how people change, and keep in mind that all the approaches that we present in this chapter address questions of change: Is the change smooth or uneven (continuous versus discontinuous)? Is this pattern of change the same for everyone, or are there many different patterns of change (one course of development versus many courses)? How do genetics and environment interact to influence development (nature versus nurture)?
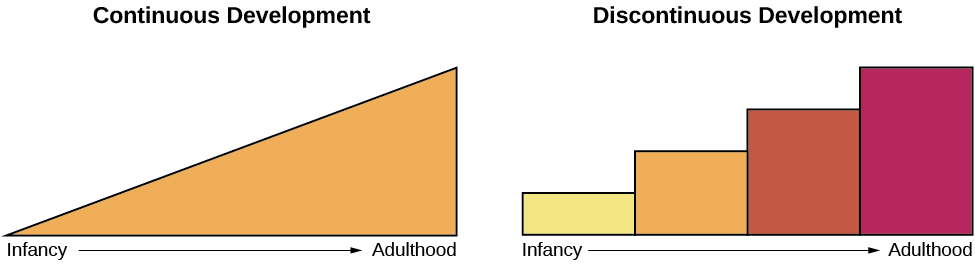
Continuous development views development as a cumulative process, gradually improving on existing skills ( [link] ). With this type of development, there is gradual change. Consider, for example, a child’s physical growth: adding inches to her height year by year. In contrast, theorists who view development as discontinuous believe that development takes place in unique stages: It occurs at specific times or ages. With this type of development, the change is more sudden, such as an infant’s ability to conceive object permanence.
Is development essentially the same, or universal, for all children (i.e., there is one course of development) or does development follow a different course for each child, depending on the child’s specific genetics and environment (i.e., there are many courses of development)? Do people across the world share more similarities or more differences in their development? How much do culture and genetics influence a child’s behavior?
Stage theories hold that the sequence of development is universal. For example, in cross-cultural studies of language development, children from around the world reach language milestones in a similar sequence (Gleitman&Newport, 1995). Infants in all cultures coo before they babble. They begin babbling at about the same age and utter their first word around 12 months old. Yet we live in diverse contexts that have a unique effect on each of us. For example, researchers once believed that motor development follows one course for all children regardless of culture. However, child care practices vary by culture, and different practices have been found to accelerate or inhibit achievement of developmental milestones such as sitting, crawling, and walking (Karasik, Adolph, Tamis-LeMonda,&Bornstein, 2010).
Are we who we are because of nature (biology and genetics), or are we who we are because of nurture (our environment and culture)? This longstanding question is known in psychology as the nature versus nurture debate. It seeks to understand how our personalities and traits are the product of our genetic makeup and biological factors, and how they are shaped by our environment, including our parents, peers, and culture. For instance, why do biological children sometimes act like their parents—is it because of genetics or because of early childhood environment and what the child has learned from the parents? What about children who are adopted—are they more like their biological families or more like their adoptive families? And how can siblings from the same family be so different?
We are all born with specific genetic traits inherited from our parents, such as eye color, height, and certain personality traits. Beyond our basic genotype, however, there is a deep interaction between our genes and our environment: Our unique experiences in our environment influence whether and how particular traits are expressed, and at the same time, our genes influence how we interact with our environment (Diamond, 2009; Lobo, 2008). This chapter will show that there is a reciprocal interaction between nature and nurture as they both shape who we become, but the debate continues as to the relative contributions of each.
Lifespan development explores how we change and grow from conception to death. This field of psychology is studied by developmental psychologists. They view development as a lifelong process that can be studied scientifically across three developmental domains: physical, cognitive development, and psychosocial. There are several theories of development that focus on the following issues: whether development is continuous or discontinuous, whether development follows one course or many, and the relative influence of nature versus nurture on development.

Notification Switch
Would you like to follow the 'Chapter 4: life span development sw' conversation and receive update notifications?