| << Chapter < Page | Chapter >> Page > |
The coercive field, H c , is the field at which the remnant magnetization is reduced to zero. This can vary from a few Am for soft magnets to 10 7 Am for hard magnets. It is the point of magnetization reversal in the sample, where the barrier between the two states of magnetization is reduced to zero by the applied field allowing the system to make a Barkhausen jump to a lower energy. It is a general indicator of the energy gradients in the sample which oppose large changes of magnetization.
The reversal of magnetization can come about as a rotation of the magnetization in a large volume or through the movement of domain walls under the pressure of the applied field. In general materials with few or no domains have a high coercivity whilst those with many domains have a low coercivity. However, domain wall pinning by physical defects such as vacancies, dislocations and grain boundaries can increase the coercivity.

The loop illustrated in [link] is indicative of a simple bi-stable system. There are two energy minima: one with magnetization in the positive direction, and another in the negative direction. The depth of these minima is influenced by the material and its geometry and is a further parameter in the strength of the coercive field. Another is the angle, Θ H , between the anisotropy axis and the applied field. The above fig shows how the shape of the hysteresis loop and the magnitude of H c varies with Θ H . This effect shows the importance of how samples with strong anisotropy are mounted in a magnetometer when comparing loops.
A hysteresis curve gives information about a magnetic system by varying the applied field but important information can also be gleaned by varying the temperature. As well as indicating transition temperatures, all of the main groups of magnetic ordering have characteristic temperature/magnetization curves. These are summarized in [link] and [link] . At all temperatures a diamagnet displays only any magnetization induced by the applied field and a small, negative susceptibility.
The curve shown for a paramagnet ( [link] ) is for one obeying the Curie law,
![]()
and so intercepts the axis at T = 0 . This is a subset of the Curie-Weiss law,
![]()
where θ is a specific temperature for a particular substance (equal to 0 for paramagnets).
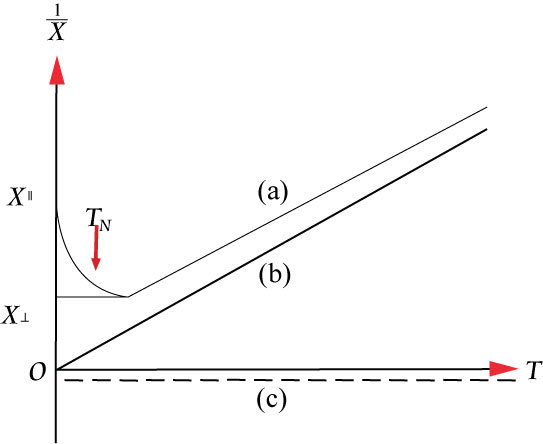

Above T N and T C both antiferromagnets and ferromagnets behave as paramagnets with 1/χ linearly proportional to temperature. They can be distinguished by their intercept on the temperature axis, T = Θ. Ferromagnetics have a large, positive Θ , indicative of their strong interactions. For paramagnetics Θ = 0 and antiferromagnetics have a negative Θ .
The net magnetic moment per atom can be calculated from the gradient of the straight line graph of 1/χ versus temperature for a paramagnetic ion, rearranging Curie's law to give

where A is the atomic mass, k is Boltzmann's constant, N is the number of atoms per unit volume and x is the gradient.
Ferromagnets below T C display spontaneous magnetization. Their susceptibility above T C in the paramagnetic region is given by the Curie-Weiss law
where g is the gyromagnetic constant. In the ferromagnetic phase with T greater than T C the magnetization M (T) can be simplified to a power law, for example the magnetization as a function of temperature can be given by
![]()
where the term β is typically in the region of 0.33 for magnetic ordering in three dimensions.
The susceptibility of an antiferromagnet increases to a maximum at T N as temperature is reduced, then decreases again below T N . In the presence of crystal anisotropy in the system this change in susceptibility depends on the orientation of the spin axes: χ (parallel)decreases with temperature whilst χ (perpendicular) is constant. These can be expressed as
![]()
where C is the Curie constant and Θ is the total change in angle of the two sublattice magnetizations away from the spin axis, and
![]()
where n g is the number of magnetic atoms per gramme, B ’ is the derivative of the Brillouin function with respect to its argument a ’ , evaluated at a ’ 0 , μ H is the magnetic moment per atom and γ is the molecular field coefficient.

Notification Switch
Would you like to follow the 'Nanomaterials and nanotechnology' conversation and receive update notifications?