| << Chapter < Page | Chapter >> Page > |
Coin production In 1942, the U.S. Mint produced 154,500,000 nickels. Write 154,500,000 in scientific notation.
Distance The distance between Earth and one of the brightest stars in the night star is 33.7 light years. One light year is about 6,000,000,000,000 (6 trillion), miles.
Debt At the end of fiscal year 2015 the gross United States federal government debt was estimated to be approximately $18,600,000,000,000 ($18.6 trillion), according to the Federal Budget. The population of the United States was approximately 300,000,000 people at the end of fiscal year 2015.
ⓐ ⓑ ⓒ
When you convert a number from decimal notation to scientific notation, how do you know if the exponent will be positive or negative?
answers will vary
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
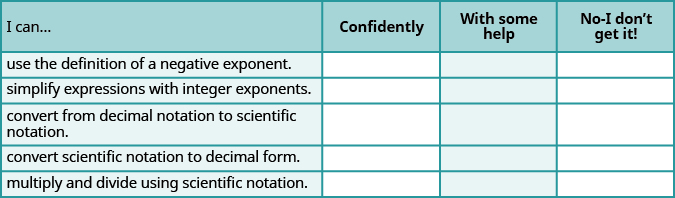
ⓑ Overall, after looking at the checklist, do you think you are well-prepared for the next section? Why or why not?
Identify Polynomials, Monomials, Binomials and Trinomials
In the following exercises, determine if each of the following polynomials is a monomial, binomial, trinomial, or other polynomial.
ⓐ
ⓑ
ⓒ
ⓓ 10
ⓔ
ⓐ
ⓑ
ⓒ
ⓓ
ⓔ
ⓐ binomial ⓑ monomial ⓒ trinomial ⓓ trinomial ⓔ other polynomial
Determine the Degree of Polynomials
In the following exercises, determine the degree of each polynomial.
Add and Subtract Monomials
In the following exercises, add or subtract the monomials.
Add and Subtract Polynomials
In the following exercises, add or subtract the polynomials.
Evaluate a Polynomial for a Given Value of the Variable
In the following exercises, evaluate each polynomial for the given value.
Evaluate when:
Randee drops a stone off the 200 foot high cliff into the ocean. The polynomial gives the height of a stone seconds after it is dropped from the cliff. Find the height after seconds.
A manufacturer of stereo sound speakers has found that the revenue received from selling the speakers at a cost of p dollars each is given by the polynomial Find the revenue received when dollars.
12,000

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?