| << Chapter < Page | Chapter >> Page > |
AKTIWITEIT 1:
Om prakties die voorwaardes van gelykvormigheid te ondersoek
1. Die vyfhoeke ABDEF en LCMRK word gegee (A-6). LCMRK is ‘n vergroting van ABDEF. Wat is die skaalfaktor waarmee ABDEF vergroot is om LCMRK te gee?
2. Skryf die verhoudings tussen die ooreenstemmende pare sye van ABDEF en LCMRK neer.
3. Skryf die verwantskap tussen die ooreenstemmende pare hoeke van die twee figure neer.
4. Hierdie twee figure is nie kongruent nie. Wat noem ons hulle?
5. Noem soveel moontlik voorbeelde in die alledaagse lewe van hierdie verskynsel.
Gelykvormige figure.
Die vyfhoeke in die aktiwiteit hierbo is gelykvormig. Hulle het dieselfde vorm, maar is nie ewe groot nie.
Hulle ooreenstemmende hoeke het dieselfde grootte.
Hulle ooreenstemmende sye is in dieselfde verhouding.
Dus is Hierdie konstante verhouding is ook die skaalfaktor van die vergroting.
Ons sê dat ABDEF LCMRK. Let daarop dat die volgorde van die letters in dieselfde volgorde van die hoeke wat gelyk is en die sye wat in verhouding is, geskryf word. (Die simbool vir gelykvormigheid is ).
Huiswerkopdrag
1. Meet die lengtes van die sye en die groottes van die hoeke in die volgende figure (A-7) en besluit of hulle gelykvormig is of nie. As die twee figure nie gelykvormig is nie, gee die rede hoekom hulle nie gelykvormig is nie.
2. As twee vierhoeke se ooreenstemmende hoeke gelyk is, is hulle noodwendig ook gelykvormig ?
3. As twee vierhoeke se sye in dieselfde verhouding is, is hulle noodwendig ook gelykvormig ?
In bostaande huiswerkopdrag het jy gesien dat, vir vierhoeke om gelykvormig te wees, aan albei voorwaardes van gelykvormigheid voldoen moet word, met ander woorde, die ooreenstemmende hoeke moet gelyk wees en die ooreenstemmende sye moet in dieselfde verhouding wees. Geld dieselfde ook vir driehoeke?
AKTIWITEIT 2:
Om prakties die voorwaardes van gelykvormigheid by driehoeke te ondersoek
[LU 3.5]
1.1
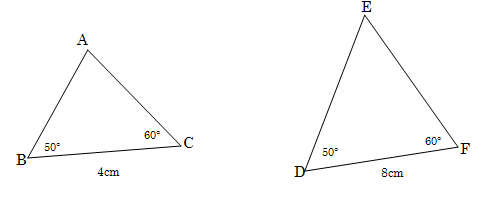
Konstrueer ΔABC en ΔDEF. Bereken die grootte van A en E.
1.2 Is die ooreenstemmende hoeke van die twee driehoeke gelyk?
1.3 Voltooi die volgende:
....................
....................
....................
1.4 Is die ooreenstemmende sye van die twee driehoeke in dieselfde verhouding?
1.5 Is die twee driehoeke gelykvormig?
1.6 Voltooi die volgende: As twee driehoeke se ooreenstemmende hoeke gelyk is, is hulle ooreenstemmende sye noodwendig altyd ......................... Dit beteken dus dat, as driehoeke se ooreenstemmende hoeke gelyk is, is die driehoeke .........................
2.1 Konstrueer die volgende twee driehoeke:

2.2 Is die sye van die twee driehoeke in dieselfde verhouding?
2.3 Meet al die hoeke van ΔABC en ΔMOR. Wat vind jy?
2.4 Is die ΔABC ΔMOR?
2.5 Voltooi die volgende: As twee driehoeke se ooreenstemmende sye in dieselfde verhouding is, is hulle ooreenstemmende ..................................... gelyk. Dit beteken dus dat, as driehoeke se ooreenstemmende sye in dieselfde verhouding is, is die driehoeke .....................................

Notification Switch
Would you like to follow the 'Wiskunde graad 9' conversation and receive update notifications?