| << Chapter < Page | Chapter >> Page > |
In 2006, Netflix issued a million dollar challenge to the world:
“Is there a computer algorithm that can accurately predict a user’s movie preferences?”
In the contest, a data matrix was given that contained ratings of thousands of movies from thousands of examinees, but it was only 2% completed. Contestants for this Netflix Challenge had to complete the matrix and provide the optimal algorithms for the task.
The Netflix Prize was won in 2009, but the ideas and algorithms generated to complete matrices remain vast and powerful in real world applications. Simply put, the Matrix Completion algorithm can be used for any areas that involve using a data matrix.
From a more scientific perspective, the 2008 paper, Exact Matrix Completion via Convex Optimization by Candes and Recht formalized a majorization minimization algorithm for matrix completion. Eric Chi’s 2014 article Getting to the Bottom of Matrix Completion and Nonnegative Least Squares with the MM Algorithm provides a more grounded framework for the problem and explains the mathematical concepts behind matrix completion.
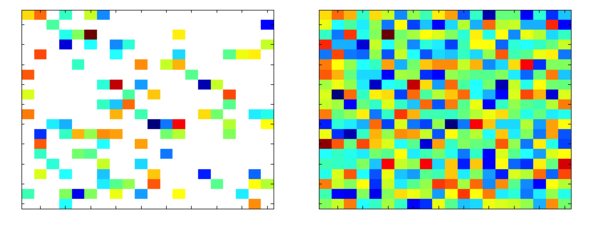
A visual representation of matrix completion.
A visual representation of matrix completion.
Given a sparse matrix with movies along one axis and users along another, the algorithm had to predict how those users would rate movies they have not seen. The solution, known as Matrix Completion, provided a good estimate of sparse data, provided it satisfied the following:
In terms of the Netflix Problem, the matrix was extremely sparse -- with millions of users and movies, less than 2% of the matrix was actually filled. The matrix also followed the above assumptions, specifically that there are a few “types” of people who watch Netflix (an action movie lover, a rom-com fanatic, etc.), making it low rank, and that each user’s reviews are spread uniformly throughout the matrix.
Often, in the real world, these idealities are not upheld. It is very rare to find a matrix that is both perfectly uniform and low rank. In order to better understand matrix completions’ application to the real world, our project aimed to stretch the second requirement and better characterize the algorithm’s limits.
Specifically, we decided to focus on the requirement that the unobserved indices in the matrix must be uniformly distributed. How uniform do the unobserved entries need to be? At what point does matrix completion “stop working”?
Even more importantly, what does a plot of the error look like as a function of uniformity? We know that non-uniform data will result in a predicted matrix that is very dissimilar to the actual matrix, and we know that uniform data will result in a predicted matrix that very similar to the actual data, but what happens in between? Does a small amount of non-uniformity result in an unusable matrix, or can matrix completion continue to work under less than ideal conditions?
While it is important to characterize algorithms to have a better theoretical understanding of how and when they work, this research has very salient real world applications as well.
Imagine an old picture with non-uniform noise distributed throughout it -- maybe one area of the photo is particularly noisy. If matrix completion can work in the conditions described previously, it would be able to reconstruct those images.
Even more importantly, matrix completion is used to predict cancer survival rates, among other medical applications. There is no guarantee that this data is uniform, but maybe matrix completion can still be trusted in these situations despite this limitation.

Notification Switch
Would you like to follow the 'Breaking matrix completion: a stress test' conversation and receive update notifications?