| << Chapter < Page | Chapter >> Page > |
If the analog signal contains frequency components that are greater than half the sampling frequency, those components will appear to be at a differentfrequency in the sampled data.
The frequency that is equal to half the sampling frequency is often referred to as the Nyquist folding frequency , or simply the folding frequency. The folding frequency is half the sampling frequency. I will provide exampleslater to illustrate where this frequency gets its name.
If a frequency component in the analog signal is less than the sampling frequency, but exceeds the folding frequency by an amount d , it will appear in the sampled data at a frequency that is the folding frequency minus d .
In other words, the entire frequency spectrum appears to fold around the folding frequency such that all frequency components that are above the folding frequency fold down to a similar position on the lower side of the foldingfrequency. Those frequency components above the folding frequency produce a mirror image below the folding frequency.
(If a frequency component in the analog signal is greater than the sampling frequency, folding still occurs, but in a more complicated way.)
Some specific numbers may make this easier to understand. Assume that the sampling frequency is 2000 samples per second, giving a folding frequency of1000 cycles per second.
If an analog signal contains a frequency component at 1100 cycles per second, it will fold down and appear at 900 cycles per second in the sampled signal.
A frequency component at 1600 cycles per second in the analog signal will fold down and appear at 400 cycles per second in the sampled signal.
A frequency component at 2000 cycles per second (the sampling frequency) will fold down and appear at zero frequency in the sampled signal.
The folding behavior is fairly easy to illustrate graphically, and I will do that shortly. Before doing that, however, I need to make a few comments aboutwhat it really means to sample an analog signal.
First we need to think about what we really have when we have a sampled time series. All that we really have is a set of values taken at specific times. Inreality, we know nothing about the values that actually existed for the analog signal in-between the samples.
For example, in the temperature experiment described earlier, when we record the temperature once every ten minutes, we can't really say what values we wouldhave recorded if we had recorded the temperature once every five minutes instead. Therefore, we sometimes find ourselves estimating what the values arebetween the recorded samples.
Consider the five plots shown in Figure 1 .
| Figure 1. Samples from five different sinusoids. |
|---|
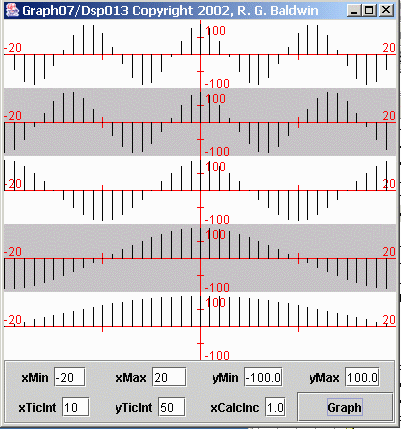 |
Figure 1 shows the values for samples taken from five different sinusoids (the height of each vertical bar represents the value of a sample).
All five sinusoids were sampled at the same sampling frequency. The sinusoid in the center was sampled twenty times per cycle (not necessarily twenty times per second).

Notification Switch
Would you like to follow the 'Digital signal processing - dsp' conversation and receive update notifications?