| << Chapter < Page | Chapter >> Page > |
Verify the divergence theorem for vector field and surface S given by the cylinder plus the circular top and bottom of the cylinder. Assume that S is positively oriented.
Both integrals equal
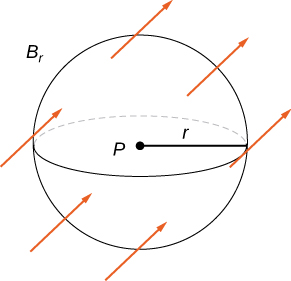
Recall that the divergence of continuous field F at point P is a measure of the “outflowing-ness” of the field at P . If F represents the velocity field of a fluid, then the divergence can be thought of as the rate per unit volume of the fluid flowing out less the rate per unit volume flowing in. The divergence theorem confirms this interpretation. To see this, let P be a point and let be a ball of small radius r centered at P ( [link] ). Let be the boundary sphere of Since the radius is small and F is continuous, for all other points Q in the ball. Therefore, the flux across can be approximated using the divergence theorem:
Since is a constant,
Therefore, flux can be approximated by This approximation gets better as the radius shrinks to zero, and therefore
This equation says that the divergence at P is the net rate of outward flux of the fluid per unit volume.
The divergence theorem translates between the flux integral of closed surface S and a triple integral over the solid enclosed by S . Therefore, the theorem allows us to compute flux integrals or triple integrals that would ordinarily be difficult to compute by translating the flux integral into a triple integral and vice versa.
Calculate the surface integral where S is cylinder including the circular top and bottom, and
We could calculate this integral without the divergence theorem, but the calculation is not straightforward because we would have to break the flux integral into three separate integrals: one for the top of the cylinder, one for the bottom, and one for the side. Furthermore, each integral would require parameterizing the corresponding surface, calculating tangent vectors and their cross product, and using [link] .
By contrast, the divergence theorem allows us to calculate the single triple integral where E is the solid enclosed by the cylinder. Using the divergence theorem and converting to cylindrical coordinates, we have
Use the divergence theorem to calculate flux integral where S is the boundary of the box given by and (see the following figure).
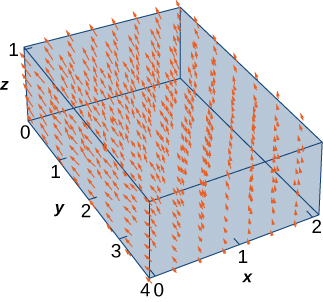
30
Let be the velocity field of a fluid. Let C be the solid cube given by and let S be the boundary of this cube (see the following figure). Find the flow rate of the fluid across S .
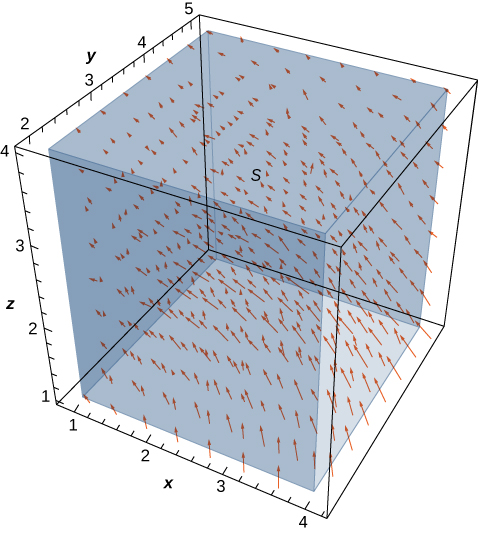
The flow rate of the fluid across S is Before calculating this flux integral, let’s discuss what the value of the integral should be. Based on [link] , we see that if we place this cube in the fluid (as long as the cube doesn’t encompass the origin), then the rate of fluid entering the cube is the same as the rate of fluid exiting the cube. The field is rotational in nature and, for a given circle parallel to the xy -plane that has a center on the z -axis, the vectors along that circle are all the same magnitude. That is how we can see that the flow rate is the same entering and exiting the cube. The flow into the cube cancels with the flow out of the cube, and therefore the flow rate of the fluid across the cube should be zero.
To verify this intuition, we need to calculate the flux integral. Calculating the flux integral directly requires breaking the flux integral into six separate flux integrals, one for each face of the cube. We also need to find tangent vectors, compute their cross product, and use [link] . However, using the divergence theorem makes this calculation go much more quickly:
Therefore the flux is zero, as expected.

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?