| << Chapter < Page | Chapter >> Page > |
A backyard deck is in the shape of an isosceles triangle with a base of feet. The perimeter of the deck is feet. How long is each of the equal sides of the deck?
14 ft
A boat’s sail is an isosceles triangle with base of meters. The perimeter is meters. How long is each of the equal sides of the sail?
7 m
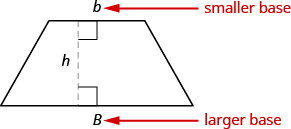
A trapezoid is four-sided figure, a quadrilateral , with two sides that are parallel and two sides that are not. The parallel sides are called the bases. We call the length of the smaller base and the length of the bigger base The height, of a trapezoid is the distance between the two bases as shown in [link] .
The formula for the area of a trapezoid is:
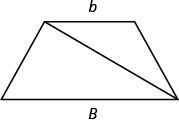
Splitting the trapezoid into two triangles may help us understand the formula. The area of the trapezoid is the sum of the areas of the two triangles. See [link] .
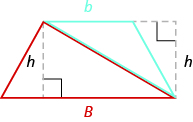
The height of the trapezoid is also the height of each of the two triangles. See [link] .
The formula for the area of a trapezoid is

If we distribute, we get,
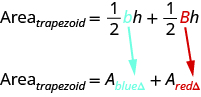
Find the area of a trapezoid whose height is 6 inches and whose bases are and inches.
| Step 1. Read the problem. Draw the figure and label it with the given information. |
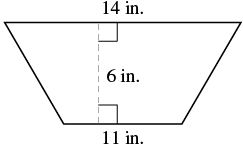 |
| Step 2. Identify what you are looking for. | the area of the trapezoid |
| Step 3. Name. Choose a variable to represent it. | Let |
| Step 4.
Translate.
Write the appropriate formula. Substitute. |
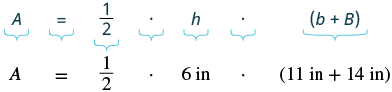 |
| Step 5. Solve the equation. |
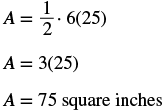 |
| Step 6. Check: Is this answer reasonable? |
If we draw a rectangle around the trapezoid that has the same big base and a height its area should be greater than that of the trapezoid.
If we draw a rectangle inside the trapezoid that has the same little base and a height its area should be smaller than that of the trapezoid.
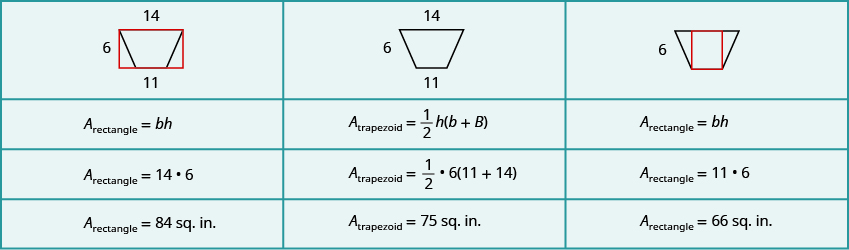
The area of the larger rectangle is square inches and the area of the smaller rectangle is square inches. So it makes sense that the area of the trapezoid is between and square inches
Step 7. Answer the question. The area of the trapezoid is square inches.
The height of a trapezoid is yards and the bases are and yards. What is the area?
161 sq. yd
The height of a trapezoid is centimeters and the bases are and centimeters. What is the area?
225 sq. cm
Find the area of a trapezoid whose height is feet and whose bases are and feet.
| Step 1. Read the problem. Draw the figure and label it with the given information. |
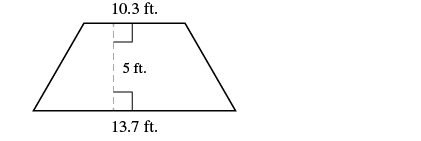 |
| Step 2. Identify what you are looking for. | the area of the trapezoid |
| Step 3. Name. Choose a variable to represent it. | Let A = the area |
| Step 4.
Translate.
Write the appropriate formula. Substitute. |
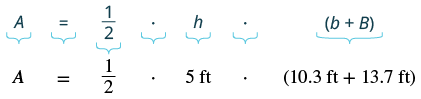 |
| Step 5. Solve the equation. |
 |
| Step 6.
Check: Is this answer reasonable?
The area of the trapezoid should be less than the area of a rectangle with base 13.7 and height 5, but more than the area of a rectangle with base 10.3 and height 5. 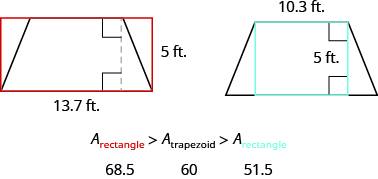 |
|
| Step 7. Answer the question. | The area of the trapezoid is 60 square feet. |

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?