| << Chapter < Page | Chapter >> Page > |
Find the ⓐ perimeter and ⓑ area of the figure:

Find the ⓐ perimeter and ⓑ area of the figure:

A rectangle has four sides and four right angles. The opposite sides of a rectangle are the same length. We refer to one side of the rectangle as the length, and the adjacent side as the width, See [link] .
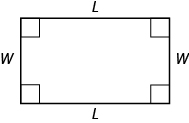
The perimeter, of the rectangle is the distance around the rectangle. If you started at one corner and walked around the rectangle, you would walk units, or two lengths and two widths. The perimeter then is
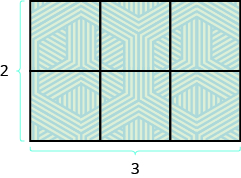
What about the area of a rectangle? Remember the rectangular rug from the beginning of this section. It was feet long by feet wide, and its area was square feet. See [link] . Since we see that the area, is the length, times the width, so the area of a rectangle is
For easy reference as we work the examples in this section, we will restate the Problem Solving Strategy for Geometry Applications here.
The length of a rectangle is meters and the width is meters. Find ⓐ the perimeter, and ⓑ the area.
| ⓐ | |
| Step 1. Read the problem. Draw the figure and label it with the given information. |
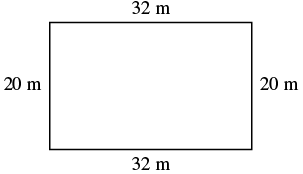 |
| Step 2. Identify what you are looking for. | the perimeter of a rectangle |
| Step 3. Name. Choose a variable to represent it. | Let P = the perimeter |
| Step 4.
Translate.
Write the appropriate formula. Substitute. |
 |
| Step 5. Solve the equation. |
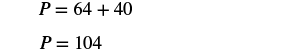 |
Step 6.
Check:
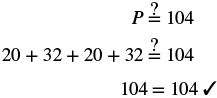 |
|
| Step 7. Answer the question. | The perimeter of the rectangle is 104 meters. |
| ⓑ | |
| Step 1. Read the problem. Draw the figure and label it with the given information. |
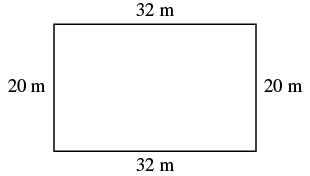 |
| Step 2. Identify what you are looking for. | the area of a rectangle |
| Step 3. Name. Choose a variable to represent it. | Let A = the area |
| Step 4.
Translate.
Write the appropriate formula. Substitute. |
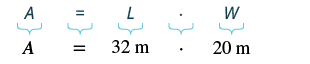 |
| Step 5. Solve the equation. |
|
Step 6.
Check:
 |
|
| Step 7. Answer the question. | The area of the rectangle is 60 square meters. |
The length of a rectangle is yards and the width is yards. Find ⓐ the perimeter and ⓑ the area.

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?