| << Chapter < Page | Chapter >> Page > |
Suppose the pair has joint density . Determine the density for
SOLUTION
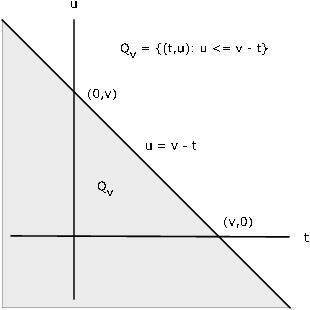
For any fixed v , the region Q v is the portion of the plane on or below the line (see [link] ). Thus
Differentiating with the aid of the fundamental theorem of calculus, we get
This integral expresssion is known as a convolution integral .
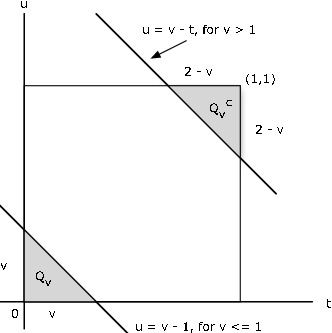
Suppose the pair has joint uniform density on the unit square , . Determine the density for .
SOLUTION
is the probability in the region . Now , where the complementary set Q v c is the set of points above the line. As Figure 3 shows, for , the part of Q v which has probability mass is the lower shaded triangular region on the figure, which has area (and hence probability) . For , the complementary region Q v c is the upper shaded region. It has area . so that in this case,
. Thus,
Differentiation shows that Z has the symmetric triangular distribution on , since
With the use of indicator functions, these may be combined into a single expression
ALTERNATE SOLUTION
Since , we have . Now iff , so that
Integration with respect to t gives the result above.
Independence of functions of independent random variables
Suppose is an independent pair. Let . Since
the pair is independent for each pair . Thus, the pair is independent.
If is an independent pair and , then the pair is independent. However, if and , then in general is not independent. This is illustrated for simple random variables with the aid of the m-procedure jointzw at the end of the next section.
Suppose is an independent pair with simple approximations X s and Y s as described in Distribution Approximations.
As functions of X and Y , respectively, the pair is independent. Also each pair is independent.
In the single-variable case, we use array operations on the values of X to determine a matrix of values of . In the two-variable case, we must use array operations on the calculating matrices t and u to obtain a matrix G whose elements are . To obtain the distribution for , we may use the m-function csort on G and the joint probability matrix P . A first step, then, is the use of jcalc or icalc to set up the joint distribution andthe calculating matrices. This is illustrated in the following example.

Notification Switch
Would you like to follow the 'Applied probability' conversation and receive update notifications?