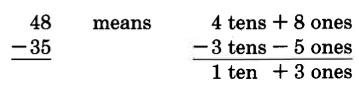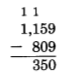This module is from Fundamentals of Mathematics by Denny Burzynski and Wade Ellis, Jr. This module discusses how to subtract whole numbers. By the end of this module, students should be able to understand the subtraction process, subtract whole numbers, and use a calculator to subtract one whole number from another whole number.
Section overview
- Subtraction
- Subtraction as the Opposite of Addition
- The Subtraction Process
- Subtraction Involving Borrowing
- Borrowing From Zero
- Calculators
Subtraction
Subtraction
Subtraction is the process of determining the remainder when part of the total is removed.
Suppose the sum of two whole numbers is 11, and from 11 we remove 4. Using the number line to help our visualization, we see that if we are located at 11 and move 4 units to the left, and thus remove 4 units, we will be located at 7. Thus, 7 units remain when we remove 4 units from 11 units.

The minus symbol
The
minus symbol (-) is used to indicate subtraction. For example,
indicates that 4 is to be subtracted from 11.
Minuend
The number immediately in front of or the minus symbol is called the
minuend , and it represents the
original number of units.
Subtrahend
The number immediately following or below the minus symbol is called the
subtrahend , and it represents the number of units
to be removed .
Difference
The
result of the subtraction is called the
difference of the two numbers. For example, in
, 11 is the minuend, 4 is the subtrahend, and 7 is the difference.
Subtraction as the opposite of addition
Subtraction can be thought of as the opposite of addition. We show this in the problems in Sample Set A.
Sample set a
Practice set a
Complete the following statements.
The subtraction process
We'll study the process of the subtraction of two whole numbers by considering the difference between 48 and 35.
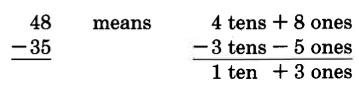
which we write as 13.
The process of subtracting whole numbers
To subtract two whole numbers,
The process
- Write the numbers vertically, placing corresponding positions in the same column.
- Subtract the digits in each column. Start at the right, in the ones position, and move to the left, placing the difference at the bottom.
Got questions? Get instant answers now!
Sample set b
Perform the following subtractions.
Got questions? Get instant answers now!
Find the difference between 977 and 235.
Write the numbers vertically, placing the larger number on top. Line up the columns properly.
The difference between 977 and 235 is 742.
Got questions? Get instant answers now!
In Keys County in 1987, there were 809 cable television installations. In Flags County in 1987, there were 1,159 cable television installations. How many more cable television installations were there in Flags County than in Keys County in 1987?
We need to determine the difference between 1,159 and 809.
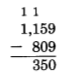
There were 350 more cable television installations in Flags County than in Keys County in 1987.
Got questions? Get instant answers now!
Practice set b
Perform the following subtractions.