| << Chapter < Page | Chapter >> Page > |
Although it wasn't apparent in Figure 7 , Figure 9 shows that the real part of the spectrum takes on the shape of a cosine wave, while the imaginary part ofthe spectrum takes on the shape of a sine wave as a result of the time delay of the impulse.
The phase shift is still linear across frequency as would be expected, but the slope is now five times greater than the slope of the phase shift in Figure 7 .
(Note that the time delay is five times greater in Figure 9 . Note also that the plot of the phase angle wraps around from +180 degrees to -180degrees each time the phase angle reaches +180 degrees. This produces the saw tooth effect shown in the bottom plot in Figure 9 .)
If an impulse is the simplest kind of pulse to generate digitally, a boxcar pulse is probably the next simplest. A "boxcar" pulse is one where severaladjacent samples have the same non-zero value. Let's examine the case for an eleven-sample boxcar pulse. The new parameters for this case are shown in Figure 10 .
| Figure 10. A boxcar pulse. |
|---|
Parameters read from file
Data length: 400Pulse length: 11
Sample for zero time: 0Lower frequency bound: 0.0
Upper frequency bound: 0.5Pulse Values
40.040.0
40.040.0
40.040.0
40.040.0
40.040.0
40.0 |
The spectral analysis output for the eleven-sample boxcar pulse is shown in Figure 11 .
| Figure 11. Spectral analysis of 11-sample boxcar pulse. |
|---|
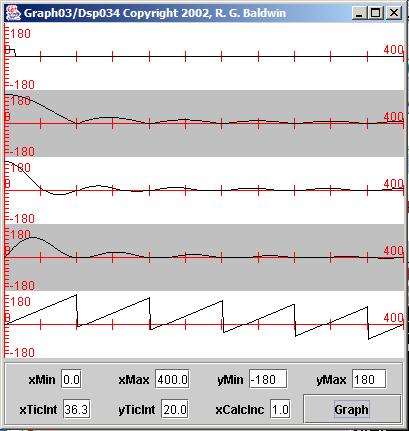 |
The pulse itself is relatively easy to see on the leftmost end of the top plot.
The amplitude spectrum is no longer flat. Rather it has a peak at zero frequency and goes to zero between frequency sample 72 and frequency sample 73.
Without getting into the technical details, I will simply tell you that the location of the point where it goes to zero is related to the reciprocal of thepulse width. If that sounds familiar, it is because we encountered similar situations involving bandwidth in the module titled Spectrum Analysis using Java, Frequency Resolution versus Data Length .
In fact, the shape of the amplitude spectrum is a familiar (sin x)/x curve with the negative lobes flipped up and turned into positive lobes instead.
The phase angle is still linear with frequency although it now shows some discontinuities at those frequencies where the amplitude spectrum touches zero.
When working with (recorded non real-time) digital time series, it is not only possible to physically shift pulses forward or backward in time, itis also possible to leave the pulses where they are and redefine the underlying time base. For the next experiment, I will leave everything else the same andredefine the location of the origin of time. I will place the time origin at themiddle of the boxcar pulse.
The new parameters for this experiment are shown in Figure 12 . Note that the only significant difference between Figure 12 and Figure 10 is the redefinition of the sample that represents zero time. I redefined the time origin from sample0 to sample 5. This causes the boxcar pulse to be centered on zero time. Five of the samples in the boxcar pulse occur in negative (history) time. One sample occurs exactly at zero time. The other five samples occur in positive (future) time .

Notification Switch
Would you like to follow the 'Digital signal processing - dsp' conversation and receive update notifications?