| << Chapter < Page | Chapter >> Page > |
We will now revisit “The Fundamental Theorem of Approximation” for the extremely important case where our set is a subspace. Specifically, suppose that is a Hilbert space, and let be a (closed) subspace of . From before, we have that for any there is a unique such that is the closest point in to . When is also a subspace, we also have:
is the minimizer of if any only if i.e., for all .
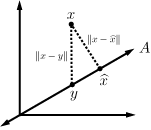
Let .
Thus , contradicting the assumption that minimizes
This result suggests a that a possible method for finding the bestapproximation to a signal from a vector space is to simply look for a vector such that . In the coming lectures we will show how to do this, but it will require a brief review of some concepts from linear algebra.

Notification Switch
Would you like to follow the 'Digital signal processing' conversation and receive update notifications?