| << Chapter < Page | Chapter >> Page > |
Some DSP processes require extremely large numbers of multiply-add operations. In order to perform DSP in real time, the equipment used to performthe arithmetic must be extremely fast. That is where the special DSP chips, (which are designed to perform multiply-add operations at an extremely high rate of speed) earn their keep.
If you plot a time series as a curve on a graph, as shown in Figure 3 , the sum of the values that make up the time series is an estimate of the net areaunder the curve.
(Assuming that the horizontal axis represents a value of zero, the sample values above the axis contribute a positive value to the net area and thesample values below the curve contribute a negative value to the net area. In the case of Figure 3 , I attempted to come up with a set of sample values that would produce a net area of zero. In other words, the area above thehorizontal axis was intended to perfectly balance the area below the horizontal axis.)
| Figure 3. Plot of values in a time series. |
|---|
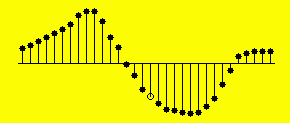 |
A periodic time series is one in which a set of sample values repeats over time, provided that you record enough samples to include one or more periods. Figure 4 shows a plot of a periodic time series. You can see that the same set of values repeats as you move from left to right on the curve plotted in Figure 4 .
| Figure 4. Area under a periodic curve. |
|---|
 |
Periodic curves can often be viewed as the sum of two curves. One of the curves is the periodic component having a zero net area under the curve whenmeasured across an even number of cycles. The other component is a constant bias offset that is added to every value of the periodic curve.
Each of the solid dark blobs in Figure 4 is a sample value. The horizontal line represents a sample value of zero. (The empty circle is the sample value half way through the sampling interval. The only reason it is different isto mark the mid point.)
What is the net area under the curve in Figure 4 ? Can you examine the curve and come up with a good estimate. As it turns out, the net area under the curvein Figure 4 is very close to zero (at least it is as close to zero as I was able to draw it) .
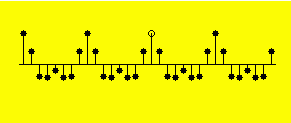
Now take a look at Figure 5 . What is the net area under the curve in Figure 5 ?
| Figure 5. Area under a periodic curve with an offset. |
|---|
 |
Each of these curves describes the same periodic shape (although Figure 4 has a larger peak-to-peak amplitude, meaning simply that every value in Figure 4 has been multiplied by the same scale factor) .
However, the curve in Figure 5 is riding up on a positive bias, while the curve in Figure 4 is centered about the horizontal axis. While the net area under the curve in Figure 4 is near zero, the net area under the curve in Figure 5 is a non-zero positive value.
The curve in Figure 5 can be considered to consist of the sum of two parts. One part is a straight horizontal line on the positive side of the horizontalaxis. The other part is the periodic curve from Figure 4 , added to that positive bias.

Notification Switch
Would you like to follow the 'Digital signal processing - dsp' conversation and receive update notifications?