| << Chapter < Page | Chapter >> Page > |
Here we look at several examples of filters designed by the Parks-McClellan algorithm. The examples here are length-15 with that shown in [link] a having a passband , a transition band , and a stopband . The number of cosine terms in the frequency response formula is , therefore, the alternation theorem says we must have at least extremal points. There are four in the passband, counting the one at zero frequency, the minimum, the maximum, andthe minimum at the bandedge. There are five in the stopband, counting the ones at the bandedge and at . So, the number is nine which is at least . However, in [link] c, there are ten extremal points but that is also at least 9, so it also is optimal. For a low pass filter, the maximum number of extremal points is and that is what this filter has. This special case is called the “maximum ripple" case.
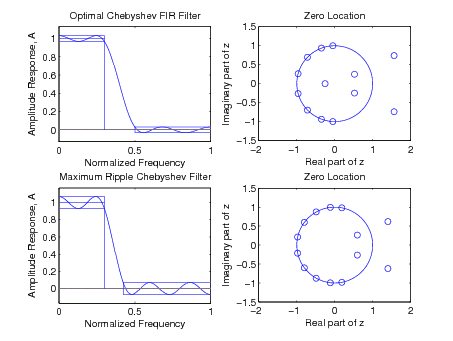
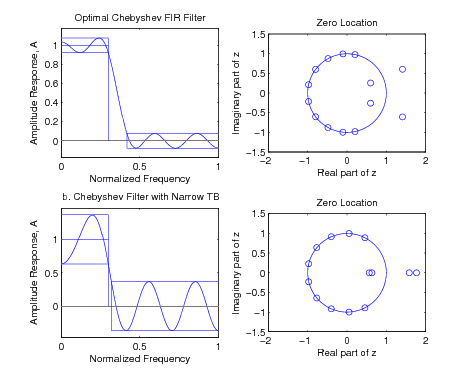
It is possible to have ripples that do not touch the maximum value and, therefore, are not considered extremal points. That is illustrated in [link] a. The effects of a narrow transitionband are illustrated in [link] c. Note the zero locations for these filters and how they relate to the amplitude response.
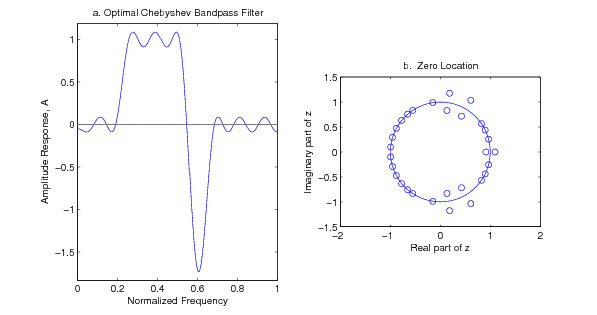
To illustrate some of the unexpected behavior that optimal filter designs can have, consider the bandpass filter amplitude response shown in [link] . Here we have a length-31 Chebyshev bandpass filter with a stopband , a transition band , a passband , another transitionband , and a stopband . The asymmetric transition bands cause large response in the transition band around . However, this filter is optimal since the deviation occurs in part of the frequency band that is not included in the optimization criterion. Ifyou think you don't care what happens in the transition bands, you may change your mind with this kind of behavior.
If one wants to fix the pass band ripple and minimize the stop band ripple [link] , equation [link] is changed so that the pass band ripple is added to the appropriate top part of the vector of the desired response and the unknown stop band is kept in the lower part of the lastcolumn of the cosine matrix .
Iteration of this equation will keep the pass band ripple fixed and minimize the stop band ripple . A problem with convergence occurs if one of the 's becomes negative during the iterations. A modification to the basic exchange has been developed to give reliableconvergence [link] .
This algorithm [link] , [link] , [link] came into existence in order to design the filters posed by Herrmann and Schüssler [link] , [link] where both the pass and stop band ripple sizes, and , are fixed and the location of the transition band is not directly controlled. Thisproblem results in a maximum ripple design which, for the lowpass filter,requires extremal frequencies at both and but does not use either pass or stop band frequencies or . This results in extremal frequencies giving equations to find the values of .

Notification Switch
Would you like to follow the 'Digital signal processing and digital filter design (draft)' conversation and receive update notifications?