| << Chapter < Page | Chapter >> Page > |
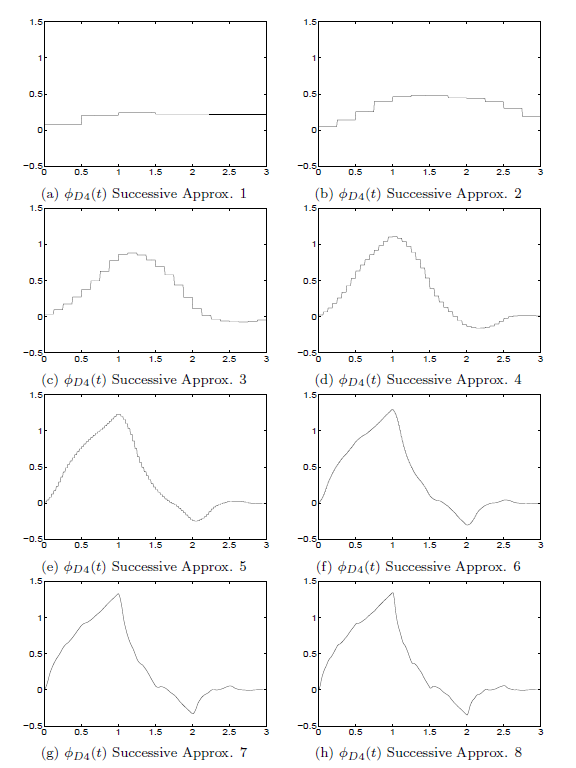
Because of the iterative form of this algorithm, applying the same process over and over, it is sometimes called the cascade algorithm [link] , [link] .
An interesting method for calculating the scaling function also uses an iterative procedure which consists of the stages of the filterstructure of Chapter: Filter Banks and the Discrete Wavelet Transform which calculates wavelet expansions coefficients (DWT values) at one scale from those at another. A scalingfunction, wavelet expansion of a scaling function itself would be a single nonzero coefficient at the scale of . Passing this single coefficient through the synthesis filter structure of Figure: Two-Stage Two-Band Synthesis Tree and [link] would result in a fine scale output that for large would essentially be samples of the scaling function.
The Fourier transform of the scaling function defined in [link] is an important tool for studying and developing wavelet theory. It could beapproximately calculated by taking the DFT of the samples of but a more direct approach is available using the infinite product in [link] . From this formulation we can see how the zeros of determine the zeros of . The existence conditions in Theorem 5 require or, more generally, for . Equation [link] gives the relation of these zeros of to the zeros of . For the index , at . For , at ,
at , etc. Because [link] is a product of stretched versions of , these zeros of are the zeros of the Fourier transform of . Recall from Theorem 15 that has no zeros in . All of this gives a picture of the shape of and the location of its zeros. From an asymptotic analysis of as , one can study the smoothness of .
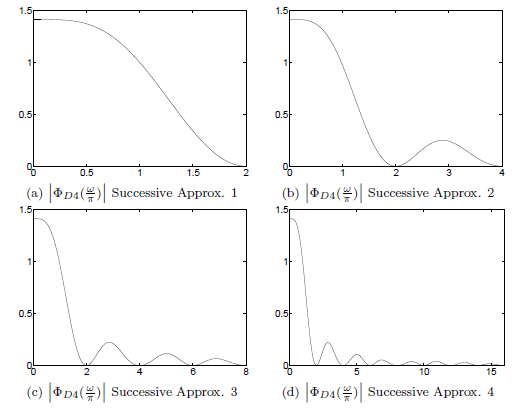
A Matlab program that calculates using this frequency domain successive approximations approach suggested by [link] is given in Appendix C . Studying this program gives further insight into the structure of . Rather than starting the calculations given in [link] for the index , they are started for the largest and worked backwards. If we calculate a length-N DFT consistent with using the FFT, then the samples of for are simply every other sample of the case for . The next stage for is done likewise and if the original is chosen a power of two, the process in continued down to without calculating any more FFTs. This results in a very efficient algorithm. The details are in theprogram itself.
This algorithm is so efficient, using it plus an inverse FFT might be a good way to calculate itself. Examples of the algorithm are illustrated in [link] where the transform is plotted for each step of the iteration.
The next method for evaluating the scaling function uses a completely different approach. It starts by calculating the values of the scalingfunction at integer values of , which can be done exactly (within our ability to solve simultaneous linear equations). Consider the basicrecursion equation [link] for integer values of

Notification Switch
Would you like to follow the 'Wavelets and wavelet transforms' conversation and receive update notifications?