Consider a latent variable,
y* , that is not observed but where
y
=
β
′
x
+
ε
.
MathType@MTEF@5@5@+=feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadMhacqGH9aqpceWHYoGbauaacaWH4bGaey4kaSIaeqyTduMaaiOlaaaa@3D72@ We want to estimate the
β
k
'
s
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabek7aInaaBaaaleaacaWGRbaabeaakiaacEcacaqGZbaaaa@3A51@ in the vector
β
=
(
β
0
β
1
⋯
β
K
)
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaahk7acqGH9aqpdaqadaqaauaabeqabqaaaaqaaiabek7aInaaBaaaleaacaaIWaaabeaaaOqaaiabek7aInaaBaaaleaacaaIXaaabeaaaOqaaiabl+Uimbqaaiabek7aInaaBaaaleaacaWGlbaabeaaaaaakiaawIcacaGLPaaacaGGUaaaaa@4431@
We may not observe
y* but we do observe:
The
μ
i
's
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabeY7aTnaaBaaaleaacaWGPbaabeaakiaabEcacaqGZbaaaa@3A63@ in (1) are parameters that must be estimated along with
β
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaahk7acaGGUaaaaa@37D9@ As usual, we assume that the error term
ε is normally distributed (with a normalized mean and variance arbitrarily set to 0 and 1, respectively). It is trivial to estimate the model with the error terms having a logistic distribution, but this chance in assumptions appears to make virtually no difference in practice).
With the normal distribution, we have:
y
=
{
0
if
y
∗
<
0
,
1
if
0
≤
y
∗
<
μ
1
,
2 if
μ
1
≤
y
∗
<
μ
2
,
⋮
J
if
μ
J
−
1
≤
y
∗
.
MathType@MTEF@5@5@+=feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadMhacqGH9aqpdaGabaabaeqabaGaaGimaiaabccacaqGGaGaaeiiaiaabMgacaqGMbGaaeiiaiaadMhadaahaaWcbeqaaiabgEHiQaaakiabgYda8iaaicdacaGGSaaabaGaaGymaiaabccacaqGGaGaaeiiaiaabMgacaqGMbGaaeiiaiaaicdacqGHKjYOcaWG5bWaaWbaaSqabeaacqGHxiIkaaGccqGH8aapcqaH8oqBdaWgaaWcbaGaaGymaaqabaGccaGGSaaabaGaaeOmaiaabccacaqGGaGaaeiiaiaabMgacaqGMbGaaeiiaiabeY7aTnaaBaaaleaacaaIXaaabeaakiabgsMiJkaadMhadaahaaWcbeqaaiabgEHiQaaakiabgYda8iabeY7aTnaaBaaaleaacaaIYaaabeaakiaacYcaaeaacqWIUlstaeaacaWGkbGaaeiiaiaabccacaqGGaGaaeyAaiaabAgacaqGGaGaeqiVd02aaSbaaSqaaiaadQeacqGHsislcaaIXaaabeaakiabgsMiJkaadMhadaahaaWcbeqaaiabgEHiQaaakiaac6caaaGaay5Eaaaaaa@70C5@
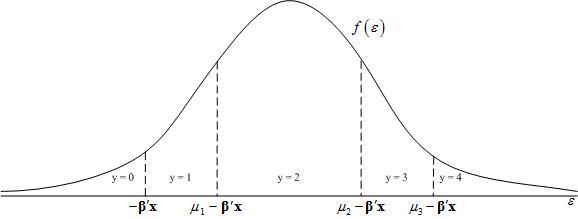
Pr
(
y
=
0
)
=
Φ
(
−
β
′
x
)
,
Pr
(
y
=
1
)
=
Φ
(
μ
1
−
β
′
x
)
−
Φ
(
−
β
′
x
)
,
Pr
(
y
=
2
)
=
Φ
(
μ
2
−
β
′
x
)
−
Φ
(
μ
1
−
β
′
x
)
,
⋮
Pr
(
y
=
J
)
=
1
−
Φ
(
μ
J
−
1
−
β
′
x
)
,
MathType@MTEF@5@5@+=feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOabaeqabaGaciiuaiaackhadaqadaqaaiaadMhacqGH9aqpcaaIWaaacaGLOaGaayzkaaGaeyypa0JaeuOPdy0aaeWaaeaacqGHsislceWHYoGbauaacaWH4baacaGLOaGaayzkaaGaaiilaaqaaiGaccfacaGGYbWaaeWaaeaacaWG5bGaeyypa0JaaGymaaGaayjkaiaawMcaaiabg2da9iabfA6agnaabmaabaGaeqiVd02aaSbaaSqaaiaaigdaaeqaaOGaeyOeI0IabCOSdyaafaGaaCiEaaGaayjkaiaawMcaaiabgkHiTiabfA6agnaabmaabaGaeyOeI0IabCOSdyaafaGaaCiEaaGaayjkaiaawMcaaiaacYcaaeaaciGGqbGaaiOCamaabmaabaGaamyEaiabg2da9iaaikdaaiaawIcacaGLPaaacqGH9aqpcqqHMoGrdaqadaqaaiabeY7aTnaaBaaaleaacaaIYaaabeaakiabgkHiTiqahk7agaqbaiaahIhaaiaawIcacaGLPaaacqGHsislcqqHMoGrdaqadaqaaiabeY7aTnaaBaaaleaacaaIXaaabeaakiabgkHiTiqahk7agaqbaiaahIhaaiaawIcacaGLPaaacaGGSaaabaGaeSO7I0eabaGaciiuaiaackhadaqadaqaaiaadMhacqGH9aqpcaWGkbaacaGLOaGaayzkaaGaeyypa0JaaGymaiabgkHiTiabfA6agnaabmaabaGaeqiVd02aaSbaaSqaaiaadQeacqGHsislcaaIXaaabeaakiabgkHiTiqahk7agaqbaiaahIhaaiaawIcacaGLPaaacaGGSaaaaaa@8C59@
where
Φ
(
⋅
)
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaahA6adaqadaqaaiabgwSixdGaayjkaiaawMcaaaaa@3AEE@ is the cumulative normal function. In order for all of the probabilities to be positive, we need
μ
1
<
μ
2
<
⋯
<
μ
J
−
1
,
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabeY7aTnaaBaaaleaacaaIXaaabeaakiabgYda8iabeY7aTnaaBaaaleaacaaIYaaabeaakiabgYda8iabl+UimjabgYda8iabeY7aTnaaBaaaleaacaWGkbGaeyOeI0IaaGymaaqabaGccaGGSaaaaa@4545@ as shown in Figure 1. One thing to note in Figure 1 is that the cutoff locations change when the values of the explanatory variables change.
Distribution of the error term in the ordered-probit model.
The estimation strategy from here follows the usual maximum likelihood method. The computer program forms the likelihood function and then chooses the values of the parameters (including the cutoffs) that maximize this likelihood function.
The estimated coefficients are not equal to the marginal effects of a change in one of the explanatory variables (as is also true with the logit and probit models). Consider the simple example Greene (1990, 704) describes. Assume that there are three categories. Then (2) becomes:
Pr
(
y
=
0
)
=
1
−
Φ
(
β
′
x
)
,
Pr
(
y
=
1
)
=
Φ
(
μ
−
β
′
x
)
−
Φ
(
−
β
′
x
)
,
Pr
(
y
=
2
)
=
1
−
Φ
(
μ
−
β
′
x
)
.
MathType@MTEF@5@5@+=feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOabaeqabaGaciiuaiaackhadaqadaqaaiaadMhacqGH9aqpcaaIWaaacaGLOaGaayzkaaGaeyypa0JaaGymaiabgkHiTiabfA6agnaabmaabaGabCOSdyaafaGaaCiEaaGaayjkaiaawMcaaiaacYcaaeaaciGGqbGaaiOCamaabmaabaGaamyEaiabg2da9iaaigdaaiaawIcacaGLPaaacqGH9aqpcqqHMoGrdaqadaqaaiabeY7aTjabgkHiTiqahk7agaqbaiaahIhaaiaawIcacaGLPaaacqGHsislcqqHMoGrdaqadaqaaiabgkHiTiqahk7agaqbaiaahIhaaiaawIcacaGLPaaacaGGSaaabaGaciiuaiaackhadaqadaqaaiaadMhacqGH9aqpcaaIYaaacaGLOaGaayzkaaGaeyypa0JaaGymaiabgkHiTiabfA6agnaabmaabaGaeqiVd0MaeyOeI0IabCOSdyaafaGaaCiEaaGaayjkaiaawMcaaiaac6caaaaa@6CF8@
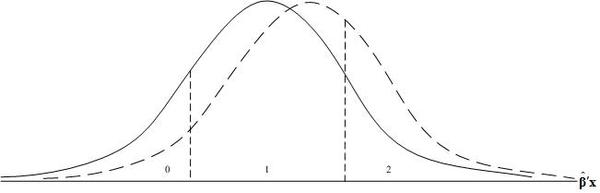
Figure 2 shows this situation. The solid curve shows the distribution of
y and
y* . Increasing one of the
x 's while holding the
β constant (that is, changing
β
^
′
x
0
MathType@MTEF@5@5@+=feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiqahk7agaqcgaqbaiaahIhadaWgaaWcbaGaaGimaaqabaaaaa@3928@ to
β
^
′
x
1
)
MathType@MTEF@5@5@+=feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiqahk7agaqcgaqbaiaahIhadaWgaaWcbaGaaGymaaqabaGccaGGPaaaaa@39E0@ is the same as shifting the entire distribution of
y and
y* to the right with
μ
^
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiqbeY7aTzaajaaaaa@37AF@ remaining constant. As a result the probabilities that y takes on the values of 0, 1, and 2 change. Clearly, as shown in Figure 2,
Pr
(
y
=
0
)
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiGaccfacaGGYbWaaeWaaeaacaWG5bGaeyypa0JaaGimaaGaayjkaiaawMcaaaaa@3BFC@ decreases and
Pr
(
y
=
2
)
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiGaccfacaGGYbWaaeWaaeaacaWG5bGaeyypa0JaaGOmaaGaayjkaiaawMcaaaaa@3BFE@ increases. The
Pr
(
y
=
1
)
,
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiGaccfacaGGYbWaaeWaaeaacaWG5bGaeyypa0JaaGymaaGaayjkaiaawMcaaiaacYcaaaa@3CAD@ on the other hand, may increase or decrease and, thus, the effect of an increase in one of the explanatory variables is ambiguous. It is easy to show this result algebraically. The marginal effects for the 3 probabilities in (3) are, assuming
β
>
0
:
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaahk7acqGH+aGpcaaIWaGaaiOoaaaa@39A7@
∂
Pr
(
y
=
0
)
∂
x
=
−
ϕ
(
β
′
x
)
β
<
0
,
∂
Pr
(
y
=
1
)
∂
x
=
ϕ
(
μ
−
β
′
x
)
β
−
ϕ
(
β
′
x
)
β
,
∂
Pr
(
y
=
2
)
∂
x
=
ϕ
(
μ
−
β
′
x
)
β
>
0.
MathType@MTEF@5@5@+=feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOabaeqabaWaaSaaaeaacqGHciITciGGqbGaaiOCamaabmaabaGaamyEaiabg2da9iaaicdaaiaawIcacaGLPaaaaeaacqGHciITcaWH4baaaiabg2da9iabgkHiTiabew9aMnaabmaabaGabCOSdyaafaGaaCiEaaGaayjkaiaawMcaaiaahk7acqGH8aapcaaIWaGaaiilaaqaamaalaaabaGaeyOaIyRaciiuaiaackhadaqadaqaaiaadMhacqGH9aqpcaaIXaaacaGLOaGaayzkaaaabaGaeyOaIyRaaCiEaaaacqGH9aqpcqaHvpGzdaqadaqaaiabeY7aTjabgkHiTiqahk7agaqbaiaahIhaaiaawIcacaGLPaaacaWHYoGaeyOeI0Iaeqy1dy2aaeWaaeaaceWHYoGbauaacaWH4baacaGLOaGaayzkaaGaaCOSdiaacYcaaeaadaWcaaqaaiabgkGi2kGaccfacaGGYbWaaeWaaeaacaWG5bGaeyypa0JaaGOmaaGaayjkaiaawMcaaaqaaiabgkGi2kaahIhaaaGaeyypa0Jaeqy1dy2aaeWaaeaacqaH8oqBcqGHsislceWHYoGbauaacaWH4baacaGLOaGaayzkaaGaaCOSdiabg6da+iaaicdacaGGUaaaaaa@7EEF@
A rise in one of the explanatory variables whose parameter is positive will shift the probability distribution of the outcome to the right (from the solid line to the dashed line).
In general, only the sign's of the change
Pr
(
y
=
0
)
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiGaccfacaGGYbWaaeWaaeaacaWG5bGaeyypa0JaaGimaaGaayjkaiaawMcaaaaa@3BFC@ and
Pr
(
y
=
J
)
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiGaccfacaGGYbWaaeWaaeaacaWG5bGaeyypa0JaamOsaaGaayjkaiaawMcaaaaa@3C11@ are unambiguous. Greene (1990, 705) cautions that "
[w]e must be very careful in interpreting the coefficients in this model.... Indeed, without a fair amount o extra calculation, it is quite unclear how the coefficients in the ordered-probit model should be interpreted. "
The bfs dataset
The data used by BFS are available at the
Journal of Applied Econometrics
data website or in the
MS Excel file
Vanderbilt data set.xls . Table 1 identifies the variables in the dataset.